Mathematics
In the figure (ii) given below, AB is a diameter of the circle whose center is O. Given that ∠ECD = ∠EDC = 32°, calculate
(i) ∠CEF
(ii) ∠COF

Answer
(i) In △EDC,
∠ECD = ∠EDC = 32° (Given)
Since sum of angles of triangle = 180°.
⇒ ∠DEC + ∠ECD + ∠EDC = 180°
⇒ ∠DEC + 32° + 32° = 180°
⇒ ∠DEC = 180° - 64°
⇒ ∠DEC = 116°.
Since, ∠CEF and ∠DEC are linear pair,
∴ ∠CEF + ∠DEC = 180°
⇒ ∠CEF + 116° = 180°
⇒ ∠CEF = 180° - 116°
⇒ ∠CEF = 64°
Hence, ∠CEF = 64°.
(ii) ∠FDC = ∠EDC = 32°. (From figure)
Arc FC subtends ∠COF at center and ∠FDC at point D of circle so,
⇒ ∠COF = 2 ∠FDC
⇒ ∠COF = 2 × 32°
⇒ ∠COF = 64°
Hence, the value of ∠COF = 64°.
Related Questions
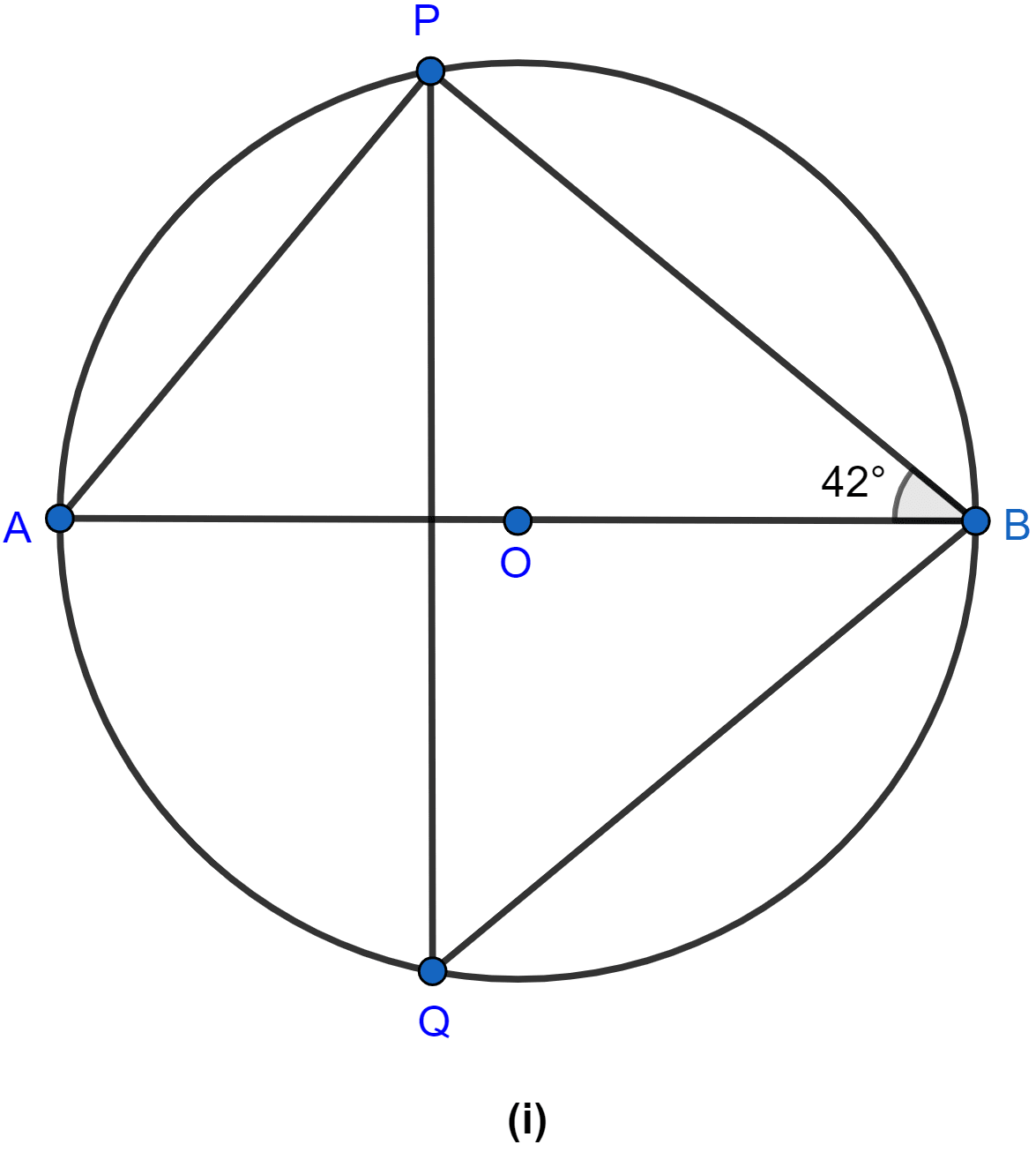
In the figure (i) given below, O is the center of the circle and ∠PBA = 42°. Calculate the value of ∠PQB.
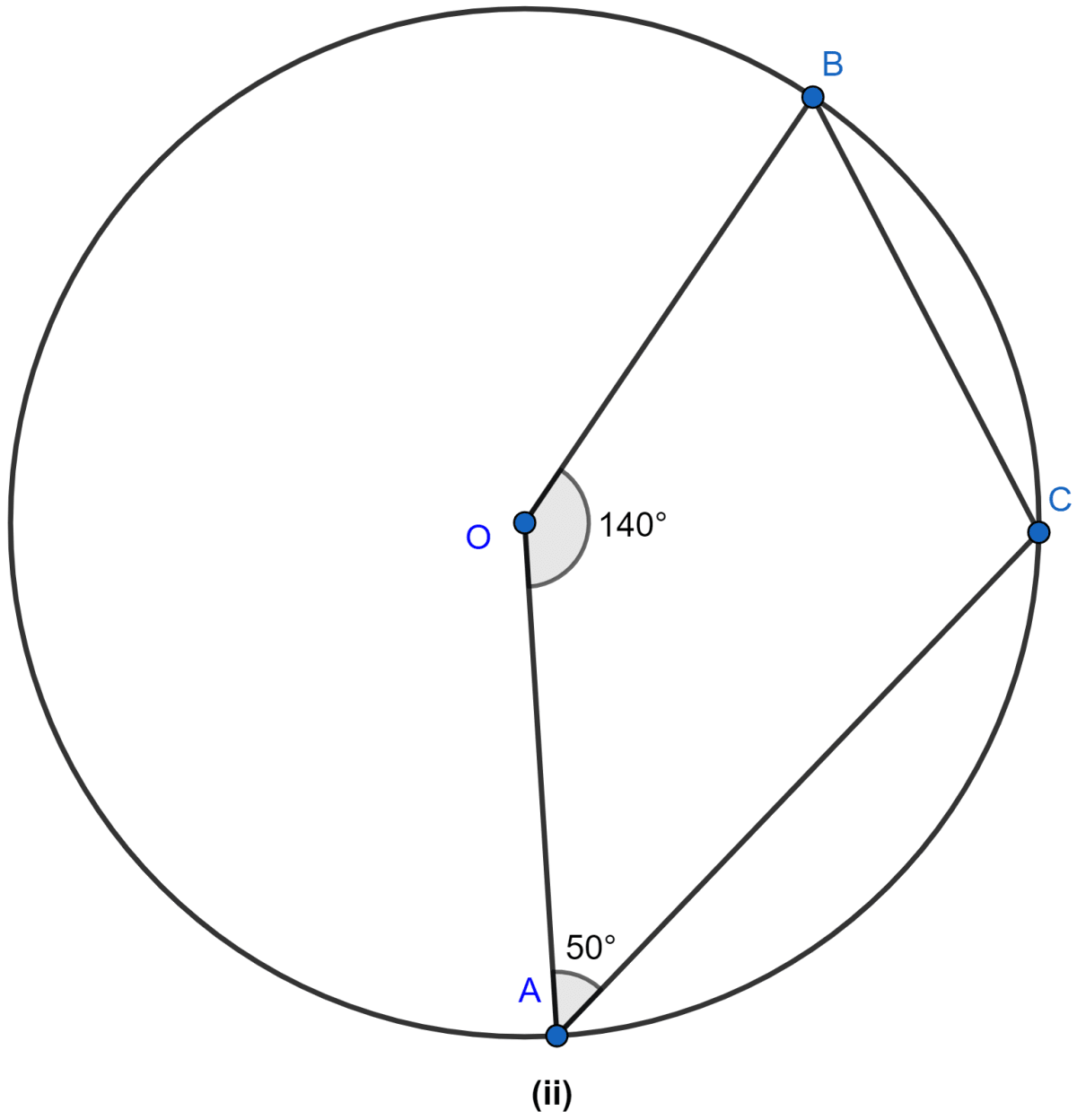
In the figure (ii) given below, O is the center of the circle. If ∠AOB = 140° and ∠OAC = 50°, find
(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA.
In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.

In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find :
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR
