Mathematics
In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.

Answer
From figure,
PT is a tangent and PA is chord.
∠APT = ∠ABP (∵ angles in alternate segments are equal.) …(i)
BDCA is a cyclic quadrilateral as all the vertices lie on the circumference of the circle.
In cyclic quadrilateral the exterior angle is equal to the opposite interior angle.
∴ ∠ABP = ∠ACD ….(ii)
From (i) and (ii),
∠APT = ∠ACD
The angles ∠APT and ∠ACD are alternate angles, but since they are equal,
Hence, proved that CD || PT.
Related Questions
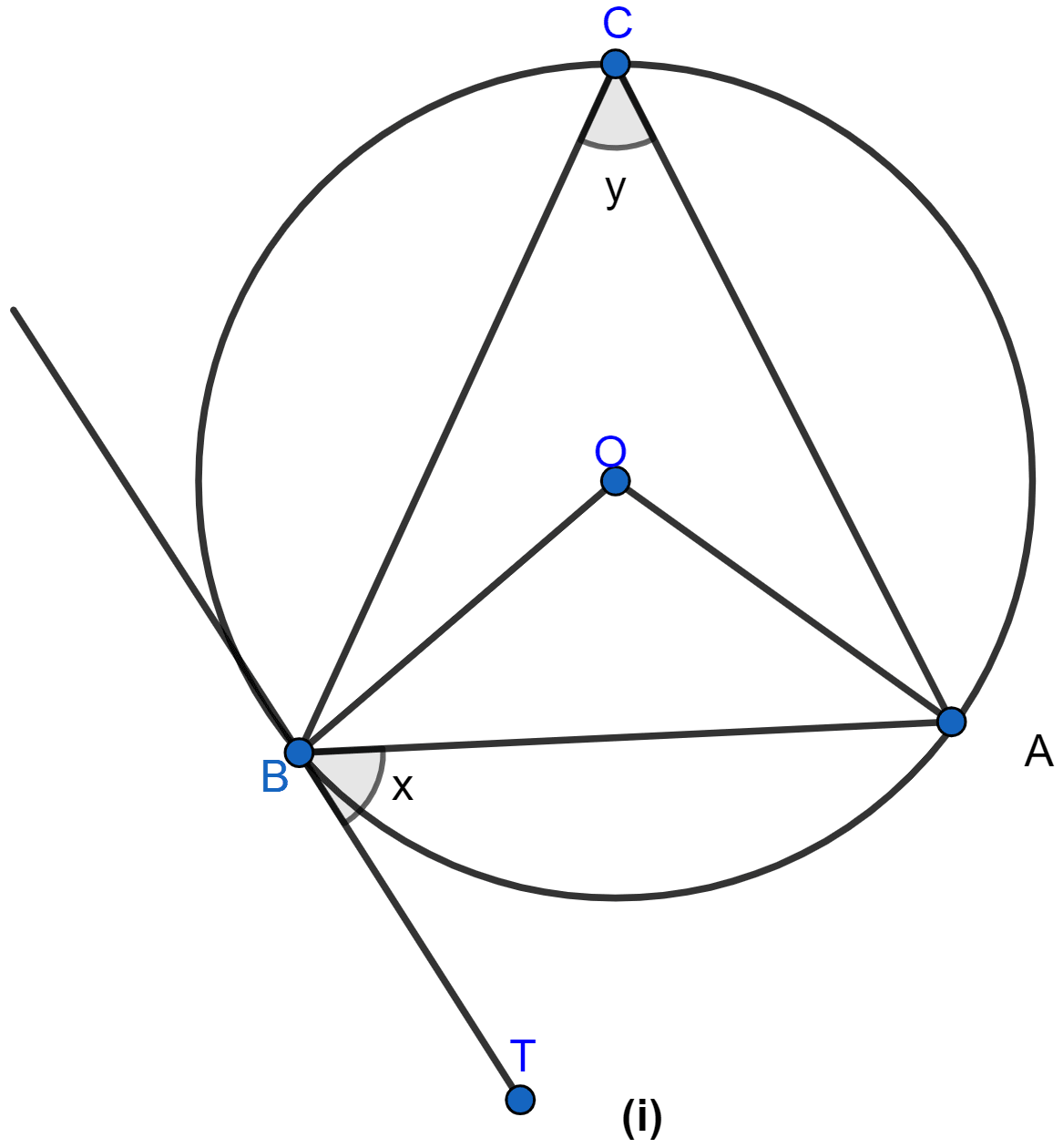
In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
In the adjoining figure, △ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of △ABC is parallel to BC.

In the figure (ii) given below, two circles with centres C, C' intersect at A, B and the point C lies on the circle with C'. PQ is a tangent to the circle with centre C' at A. Prove that AC bisects ∠PAB.

If the sides of a rectangle touch a circle, prove that the rectangle is a square.