Mathematics
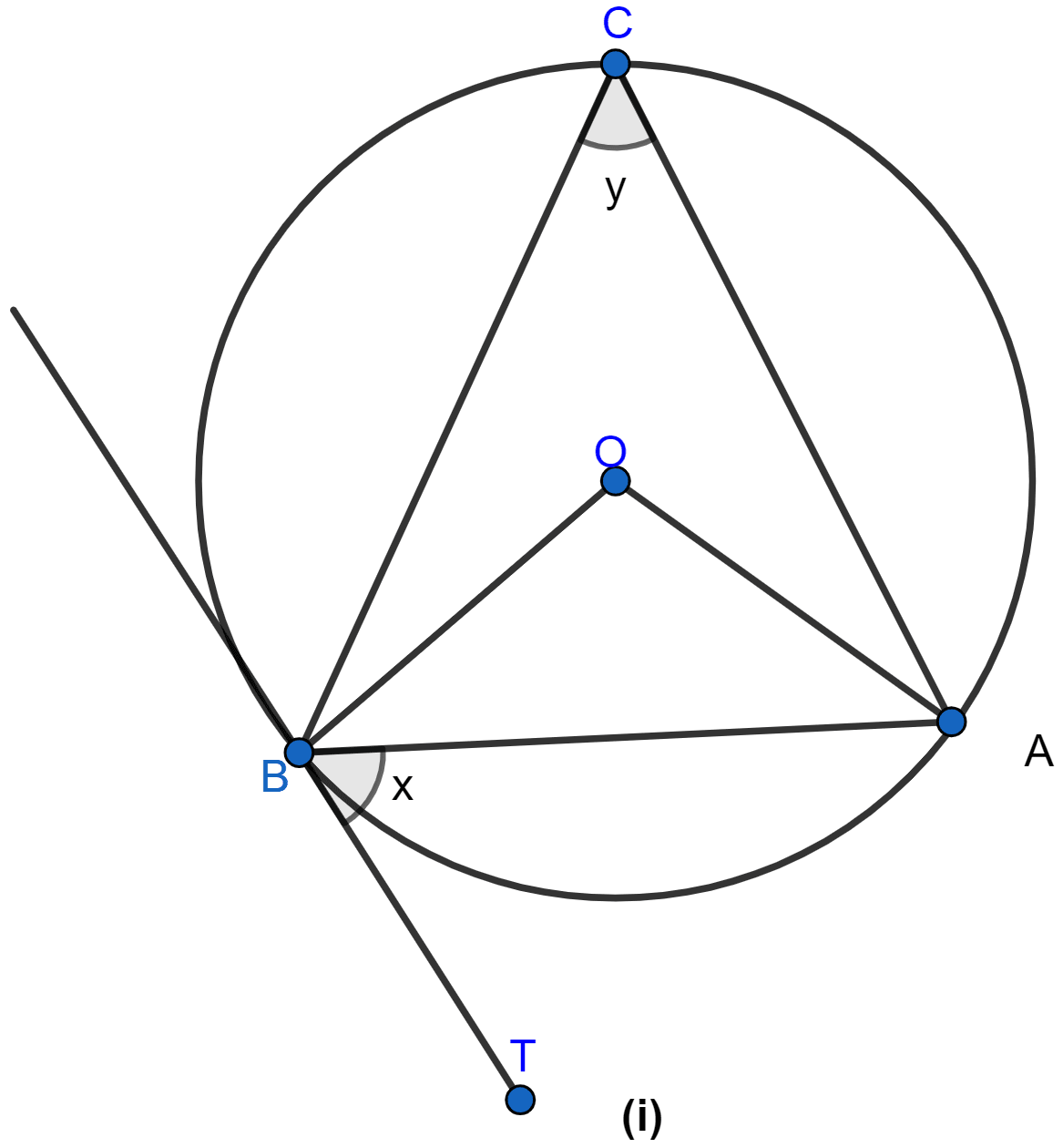
In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
Circles
14 Likes
Answer
In △OAB,
OA = OB (∵ both are radius of the common circle.)
So, △OAB is a isosceles triangle with,
∠OBA = ∠OAB = 32°.
Since sum of angles in a triangle = 180°.
In △OAB,
⇒ ∠OBA + ∠OAB + ∠AOB = 180°
⇒ 32° + 32° + ∠AOB = 180°
⇒ 64° + ∠AOB = 180°
⇒ ∠AOB = 180° - 64°
⇒ ∠AOB = 116°.
Arc AB subtends ∠AOB at centre and ∠ACB at remaining part of circle.
∴ ∠AOB = 2∠ACB (∵ angle subtended at centre is double the angle subtended at remaining part of the circle.)
⇒ 116° = 2y
⇒ y =
⇒ y = 58°.
From figure,
∠ABT = ∠ACB = 58° (∵ angles in alternate segments are equal.)
∴ x = 58°.
Hence, the value of x = 58° and y = 58°.
Answered By
8 Likes
Related Questions
In the figure (ii) given below, O and O' are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that,
(i) M bisects AB.
(ii) ∠APB = 90°.
In the figure (ii) given below, two circles with centres C, C' intersect at A, B and the point C lies on the circle with C'. PQ is a tangent to the circle with centre C' at A. Prove that AC bisects ∠PAB.
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.
