Mathematics
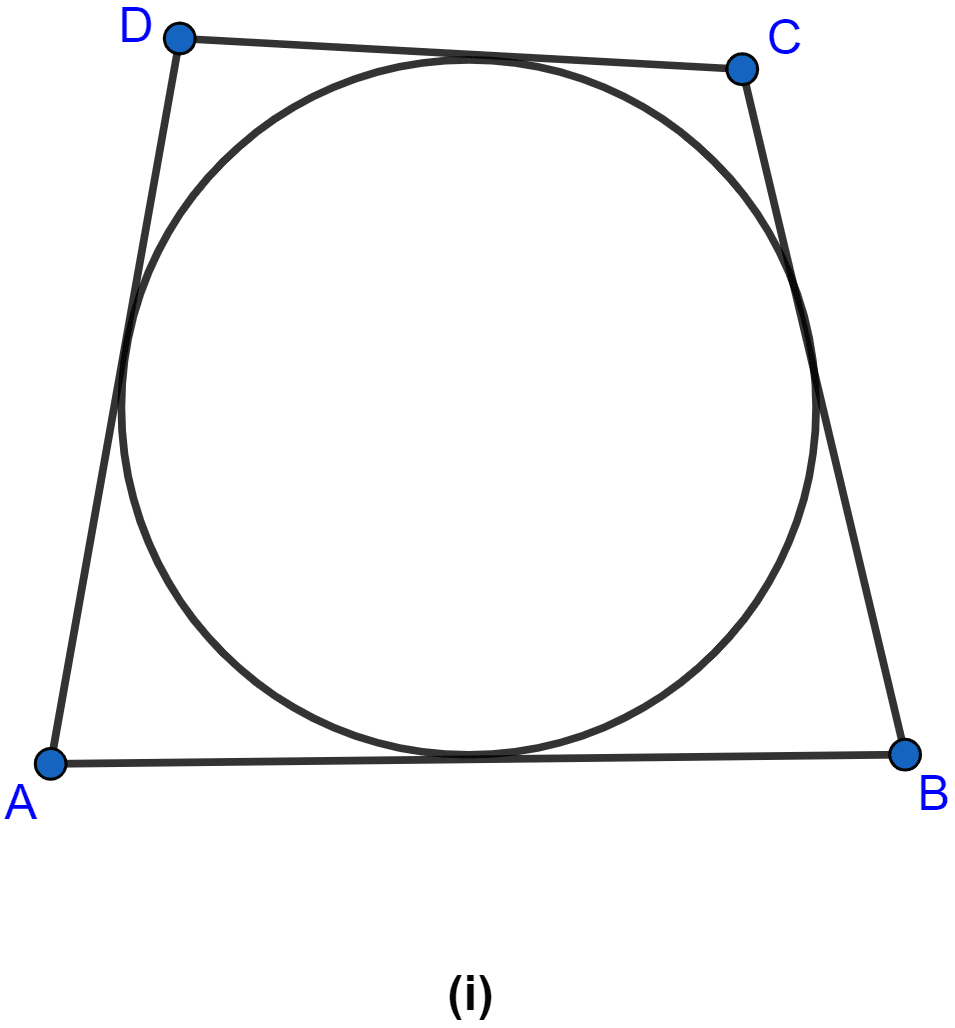
In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
Answer
Let p, Q, R, S be the points where the circle touches the sides of the quadrilateral as shown in the figure below:
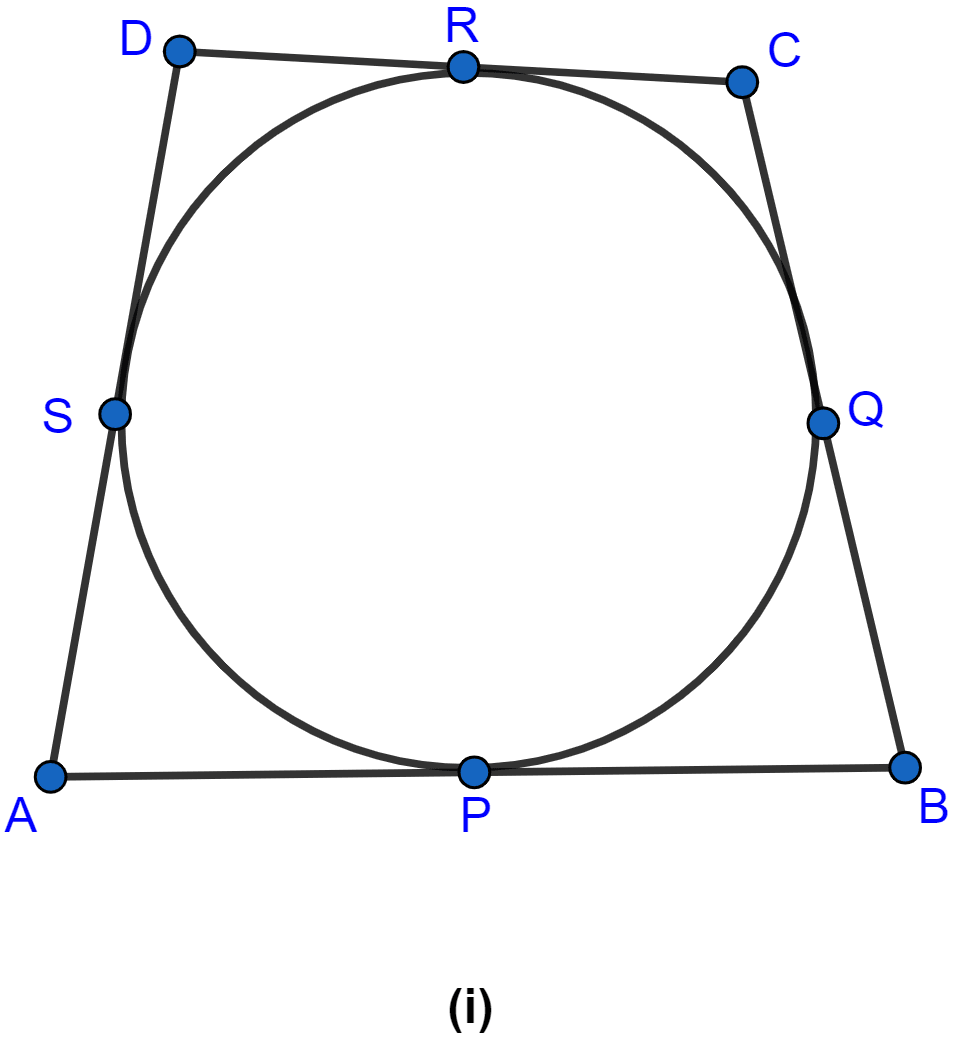
From A, AP and AS are the tangents to the circle.
∴ AP = AS …(i) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From B, BP and BQ are the tangents to the circle.
∴ PB = BQ ….(ii) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From C, CR and CQ are the tangents to the circle.
∴ CR = CQ ….(iii) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From D, DR and DS are the tangents to the circle.
∴ DR = DS ….(iv) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
Adding L.H.S. and R.H.S. of equations (i), (ii), (iii) and (iv) we get,
⇒ AP + PB + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = BC + DA
Hence, proved that AB + CD = BC + DA.
Related Questions
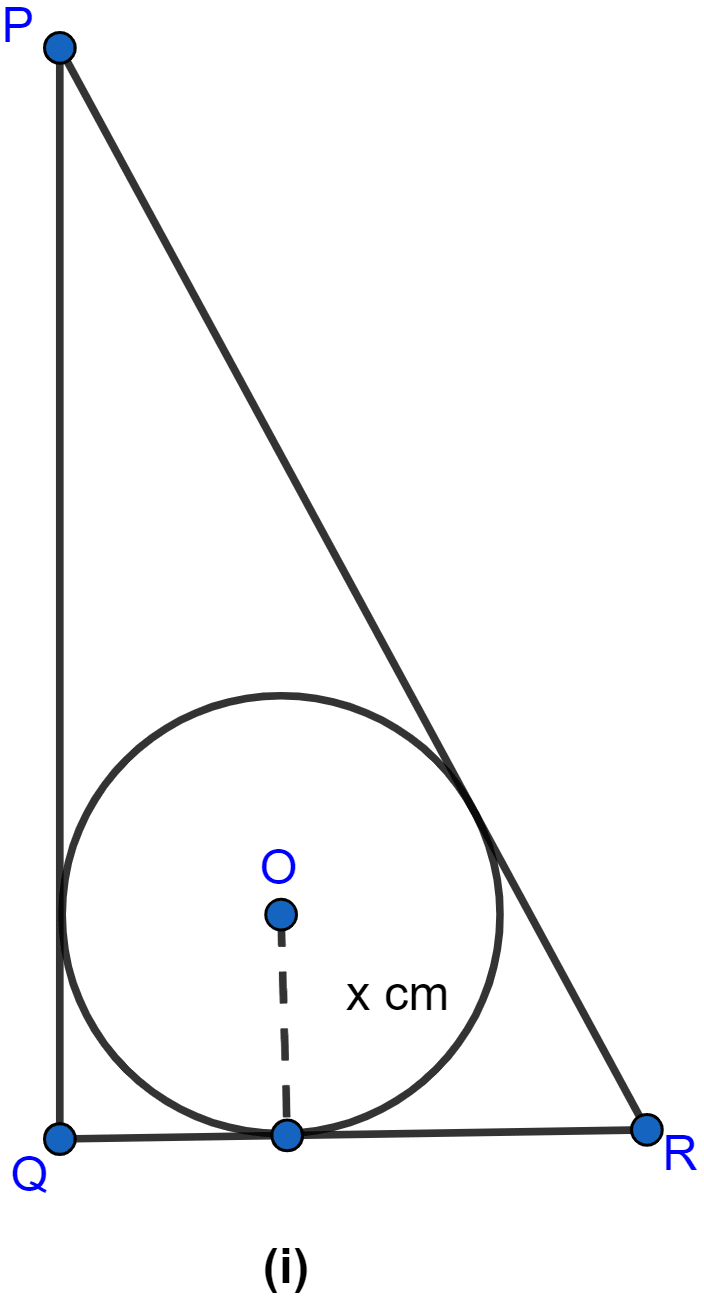
In the figure (i) given below, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle of △PQR.
In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.

Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
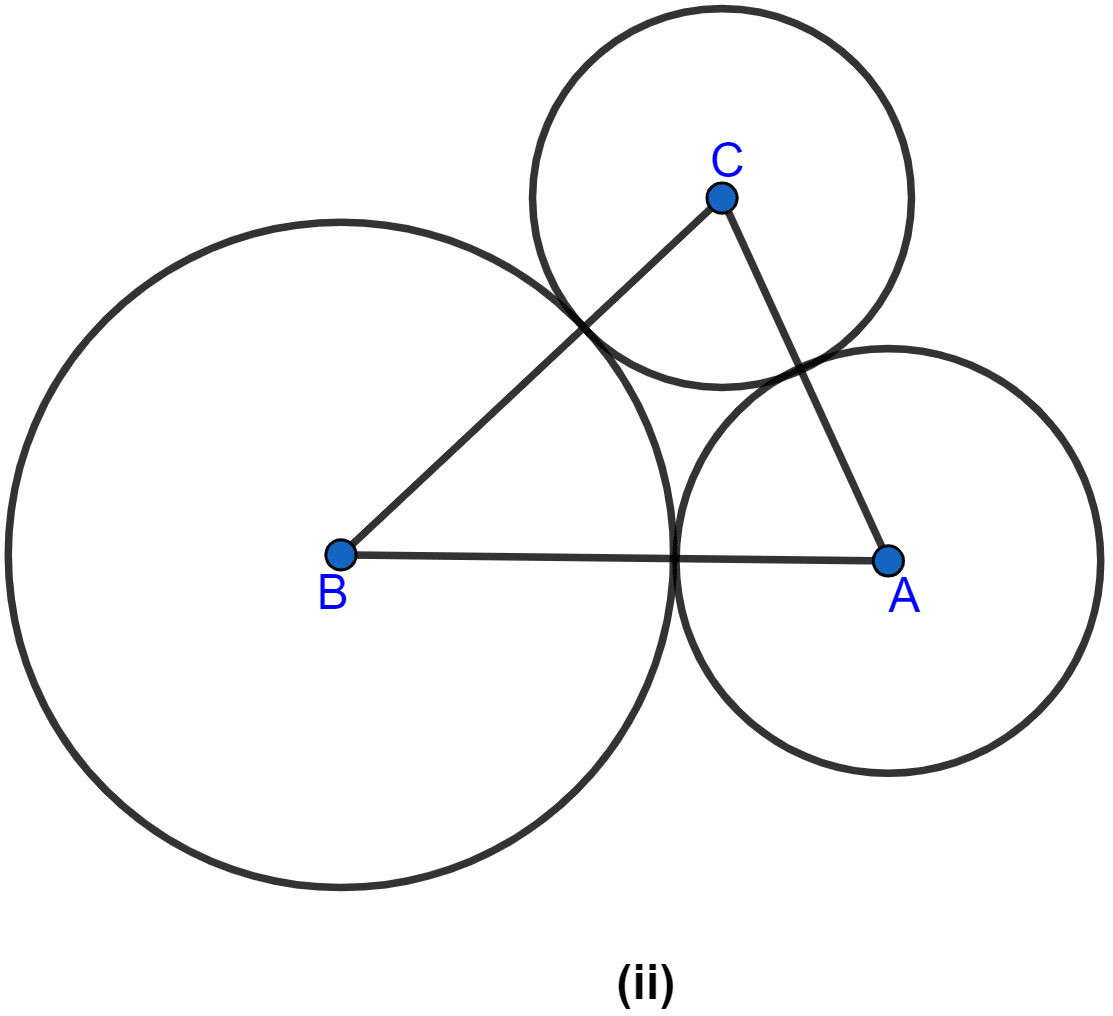
In the figure (ii) given below, ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles.