Mathematics
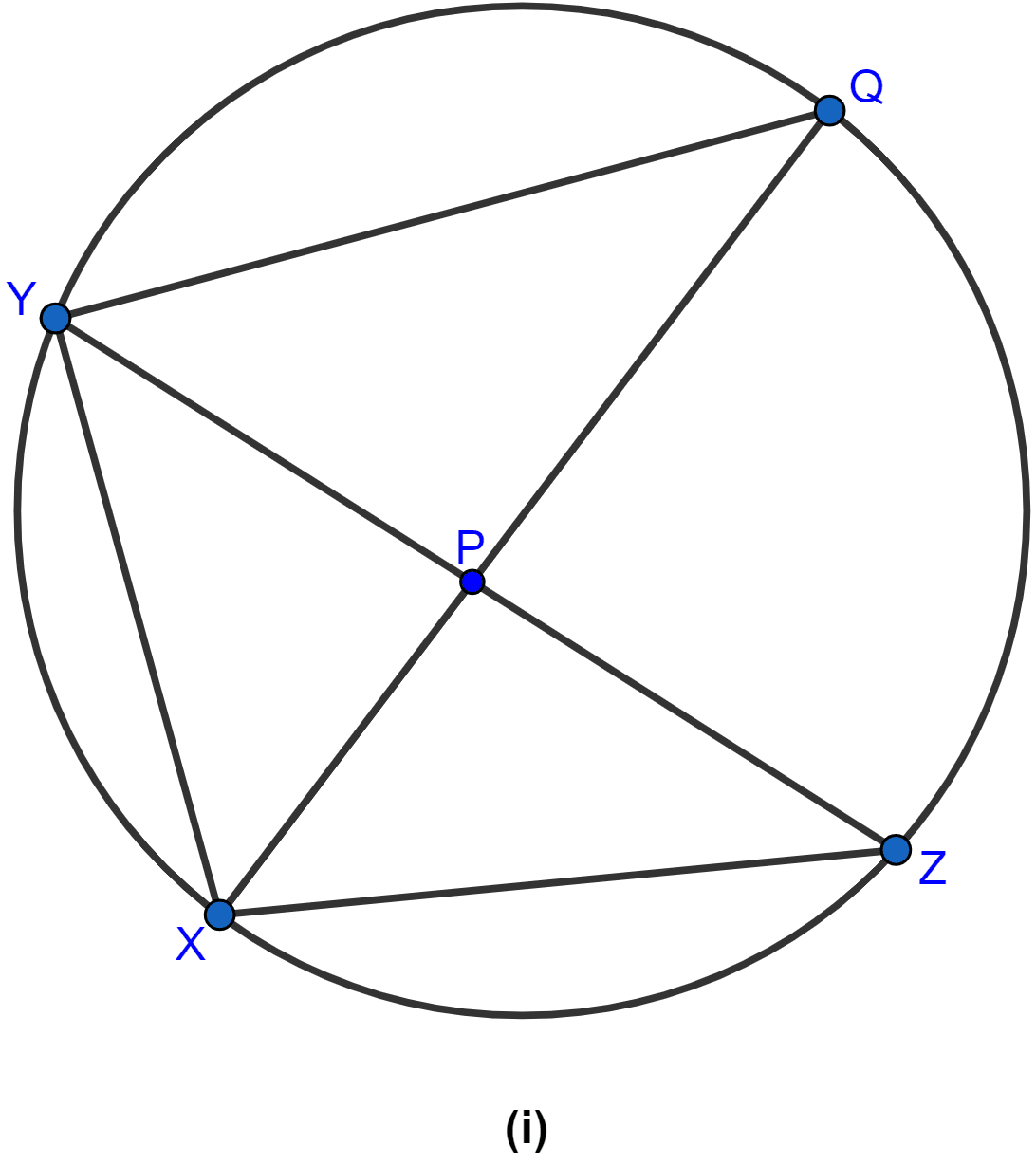
In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ.
Circles
31 Likes
Answer
In △XYQ and △XPZ,
∠Q = ∠Z (∵ angles in same segment are equal as arc XY subtends both the angles at the circle.)
∠YXQ = ∠PXZ (∵ QPX is the bisector of ∠YXZ hence it divides the angle in two equal halves.)
△XYQ ~ △XPZ. (By AA axiom)
Since triangles are similar hence, the ratio of corresponding sides are similar,
Hence, proved that XY : XQ = XP : XZ.
Answered By
20 Likes
Related Questions
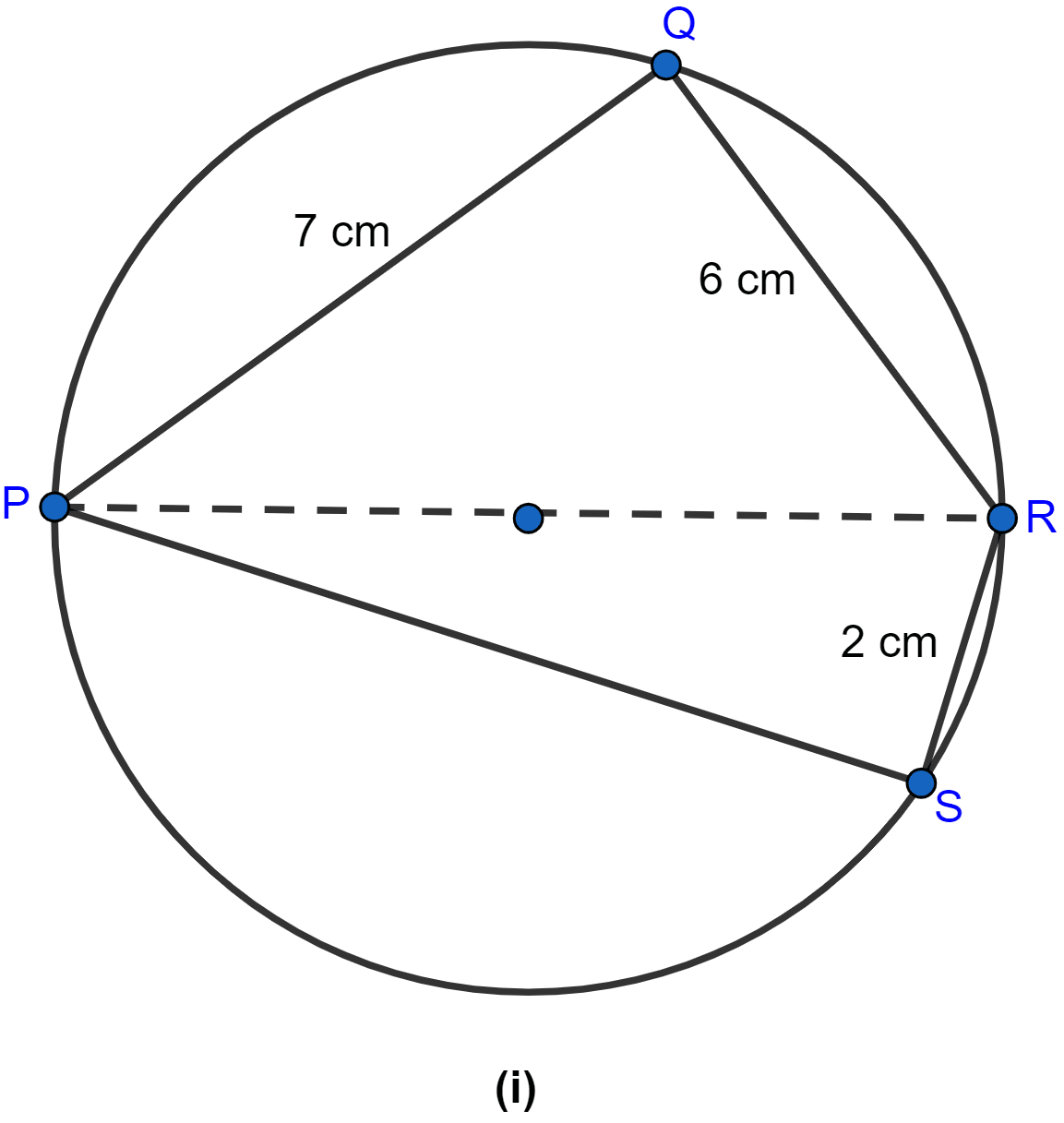
In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
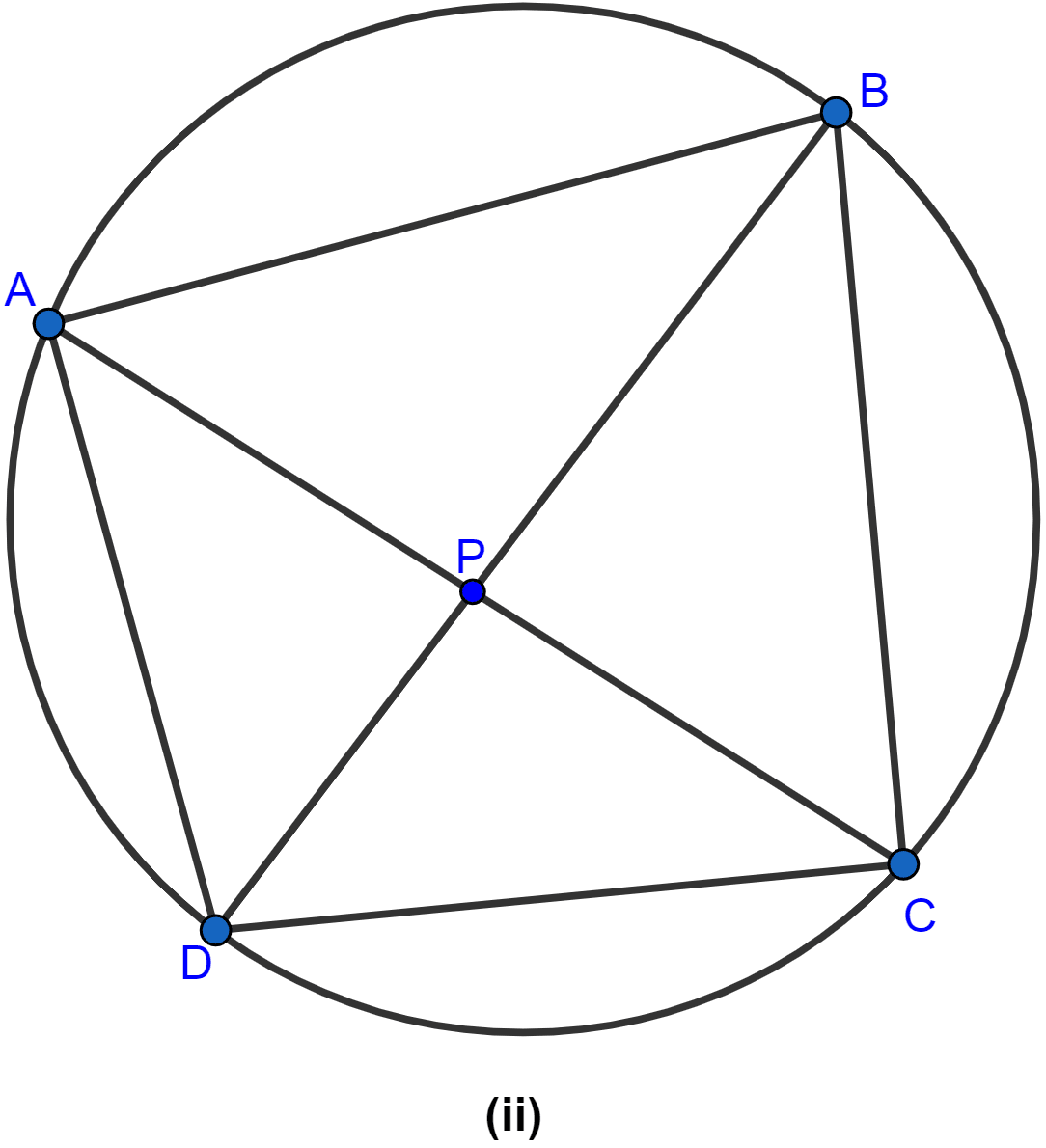
In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm2. If AB = 8 cm and CD = 5 cm, calculate the area of △DPC.
In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that
(i) ∠PAD = ∠PCB
(ii) PA × PB = PC × PD.

If O is the center of the circle find the value of x in the following figure (using the given information) :
