Mathematics
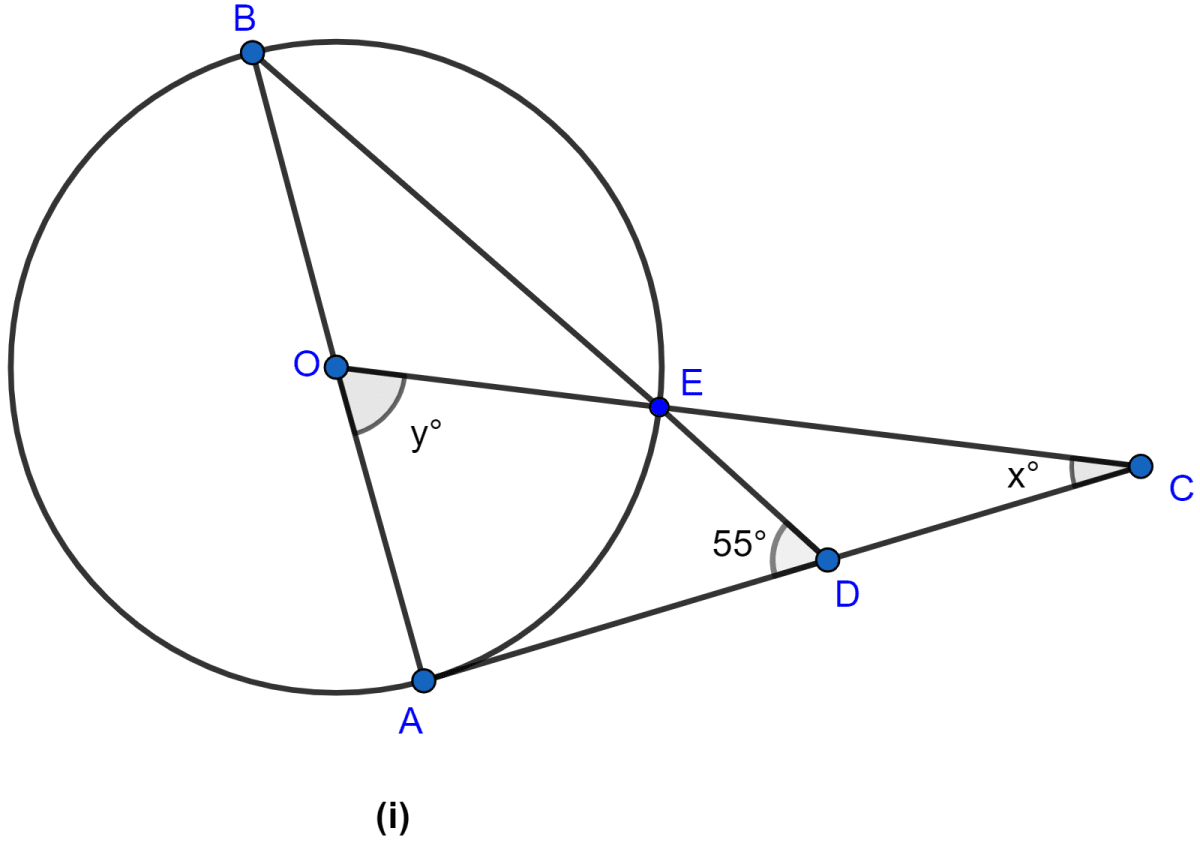
In the figure (i) given below, AC is a tangent to the circle with centre O. If ∠ADB = 55°, find x and y. Give reasons for your answers.
Answer
We know that angle between the radius and tangent at the point of contact is right angle.
∴ ∠A = 90°.
Also in △OBE, OB = OE = radius of the circle.
∴ ∠B = ∠OEB …..(i)
In △ABD,
⇒ ∠A + ∠B + ∠ADB = 180°
⇒ 90° + ∠B + 55° = 180°
⇒ ∠B + 145° = 180°
⇒ ∠B = 180° - 145° = 35°.
∴ ∠OEB = 35°.
From figure,
∠DEC = ∠OEB = 35° (∵ vertically opposite angles are equal.)
∠EDC + ∠ADE = 180° (∵ both form a linear pair)
∠EDC + 55° = 180°
∠EDC = 180° - 55°
∠EDC = 125°.
In △EDC,
⇒ ∠DEC + ∠EDC + ∠DCE = 180°
⇒ 35° + 125° + x° = 180°
⇒ x° + 160° = 180°
⇒ x° = 180° - 160° = 20°.
In △AOC,
⇒ ∠AOC + ∠OAC + ∠ACO = 180°
⇒ y° + 90° + x° = 180°
⇒ y° + 90° + 20° = 180°
⇒ y° + 110° = 180°
⇒ y° = 180° - 110° = 70°.
Hence, the value of x = 20 and y = 70.
Related Questions
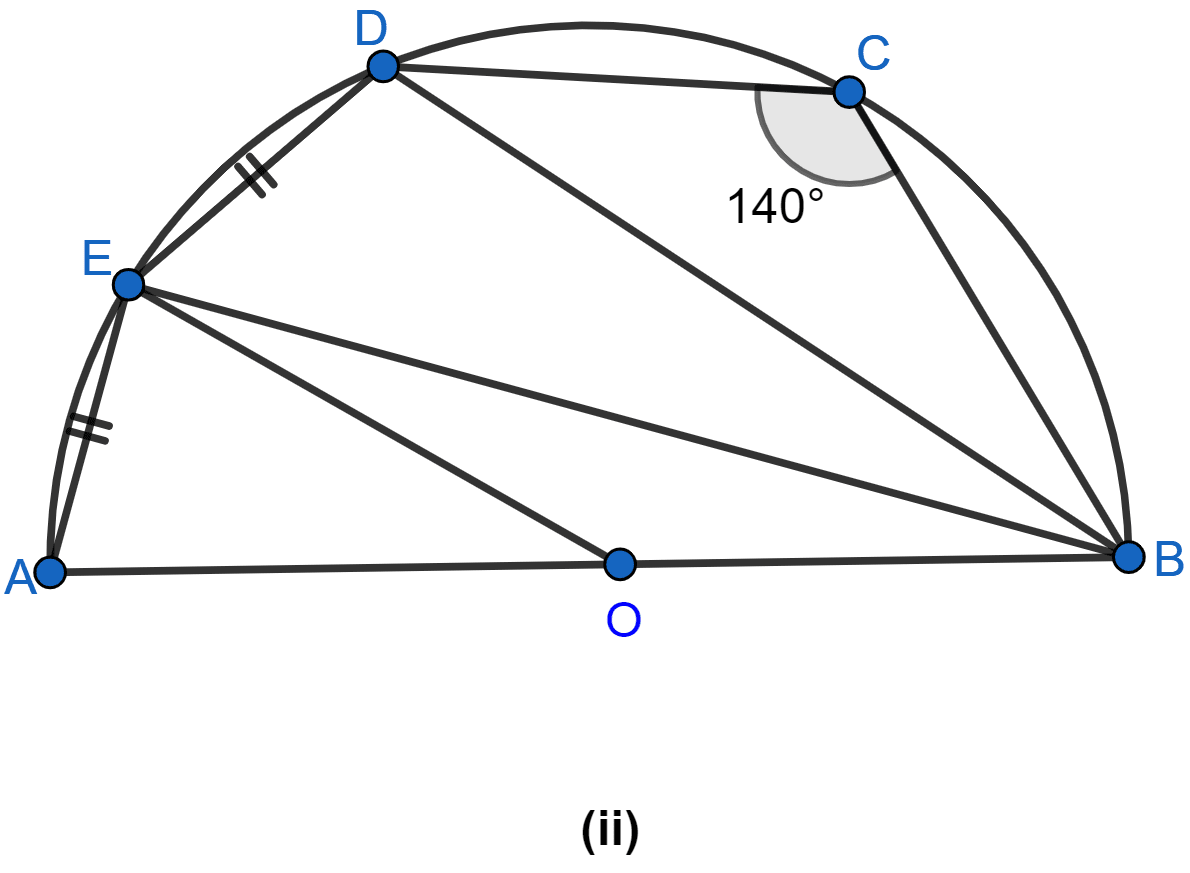
In the figure (ii) given below, AB is a diameter of the semicircle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also prove that OE is parallel to BD.
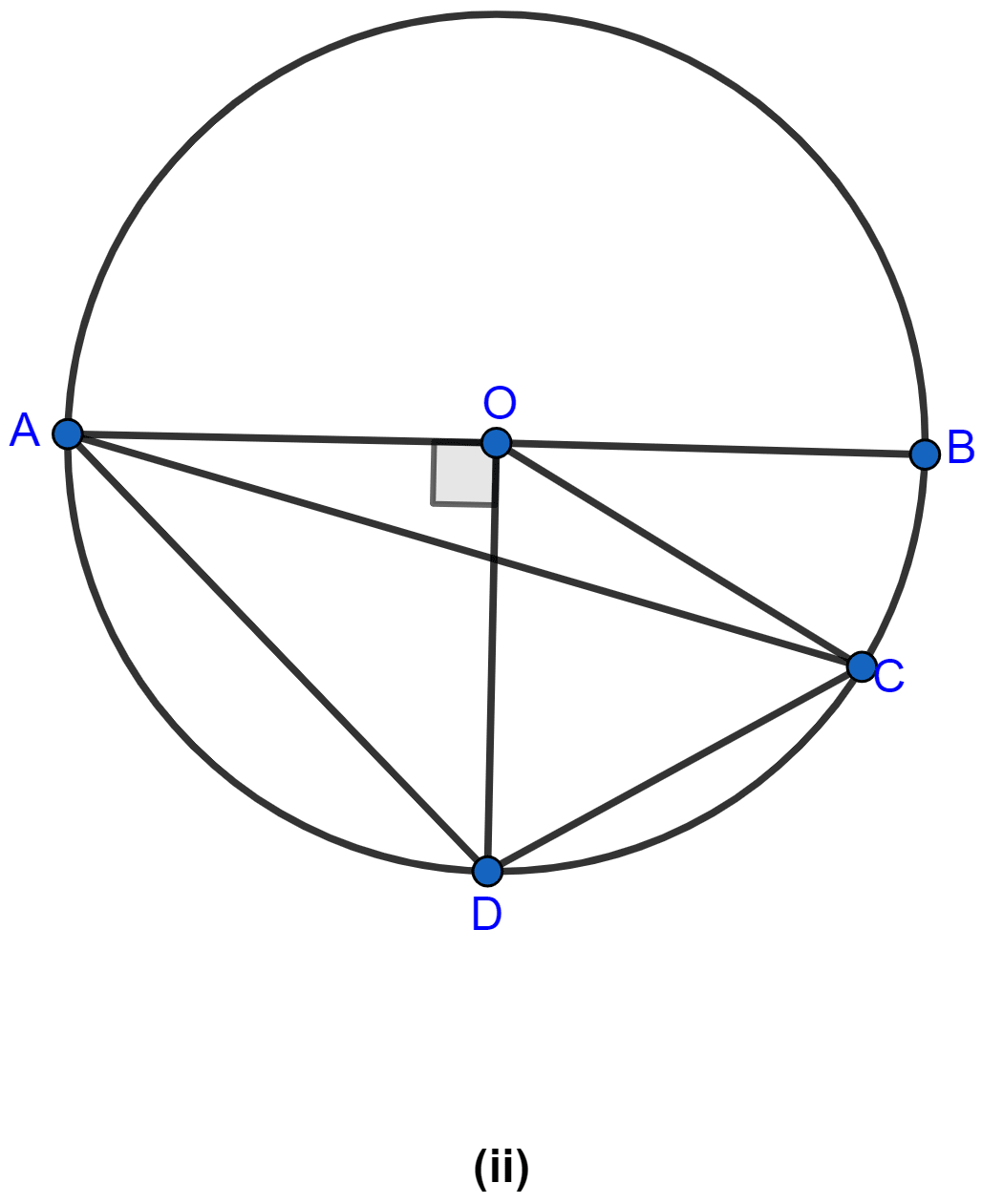
In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD.
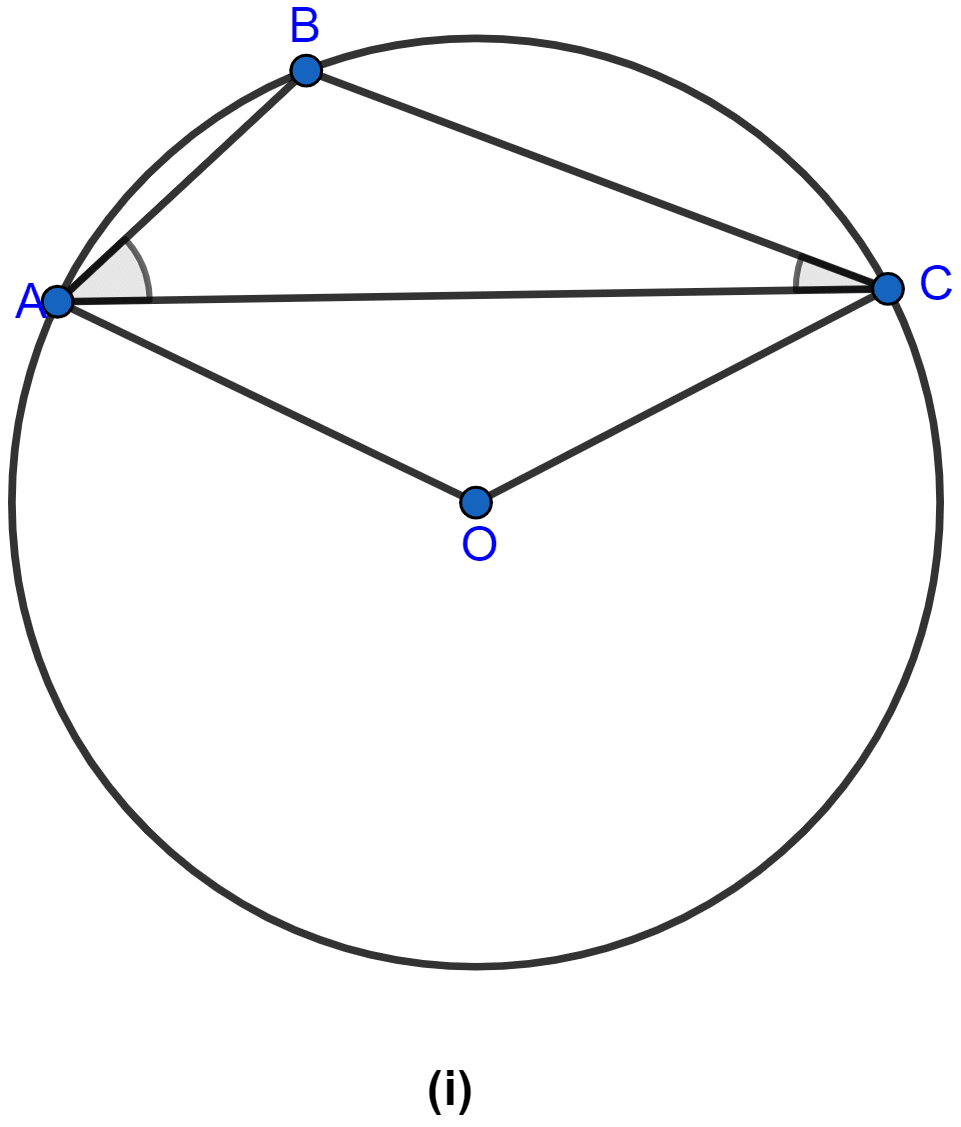
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.

In the figure (i) given below, O is the centre of the circle. Prove that ∠AOC = 2(∠ACB + ∠BAC).