Mathematics
In the figure (i) given below, AB and XY are diameters of a circle with centre O. If ∠APX = 30°, find
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX.

Circles
35 Likes
Answer
(i) Arc AX subtends ∠AOX at the centre and ∠APX at the remaining part of the circle.
⇒ ∠AOX = 2∠APX (∵ angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ ∠AOX = 2 × 30°
⇒ ∠AOX = 60°.
Hence, the value of ∠AOX = 60°.
(ii) From figure,
∠XPY = 90° (∵ angle in semicircle = 90°.)
∴ ∠APY = ∠XPY - ∠APX = 90° - 30° = 60°.
Hence, the value of ∠APY = 60°.
(iii) From figure,
∠APB = 90° (∵ angle in semicircle = 90°.)
∴ ∠BPY = ∠APB - ∠APY = 90° - 60° = 30°.
Hence, the value of ∠BPY = 30°.
(iv) In △AOX,
OA = OX (Radius of the same circle.)
∴ ∠OAX = ∠OXA
Since sum of angles of a triangle = 180°
∴ ∠AOX + ∠OAX + ∠OXA = 180°
⇒ 60° + ∠OAX + ∠OAX = 180°
⇒ 2∠OAX = 180° - 60°
⇒ 2∠OAX = 120°
⇒ ∠OAX = 60°.
Hence, the value of ∠OAX = 60°.
Answered By
24 Likes
Related Questions
In the figure (i) given below, chords AB, BC and CD of a circle with center O are equal. If ∠BCD = 120°, find
(i) ∠BDC
(ii) ∠BEC
(iii) ∠AEB
(iv) ∠AOB.
Hence, prove that △OAB is equilateral.

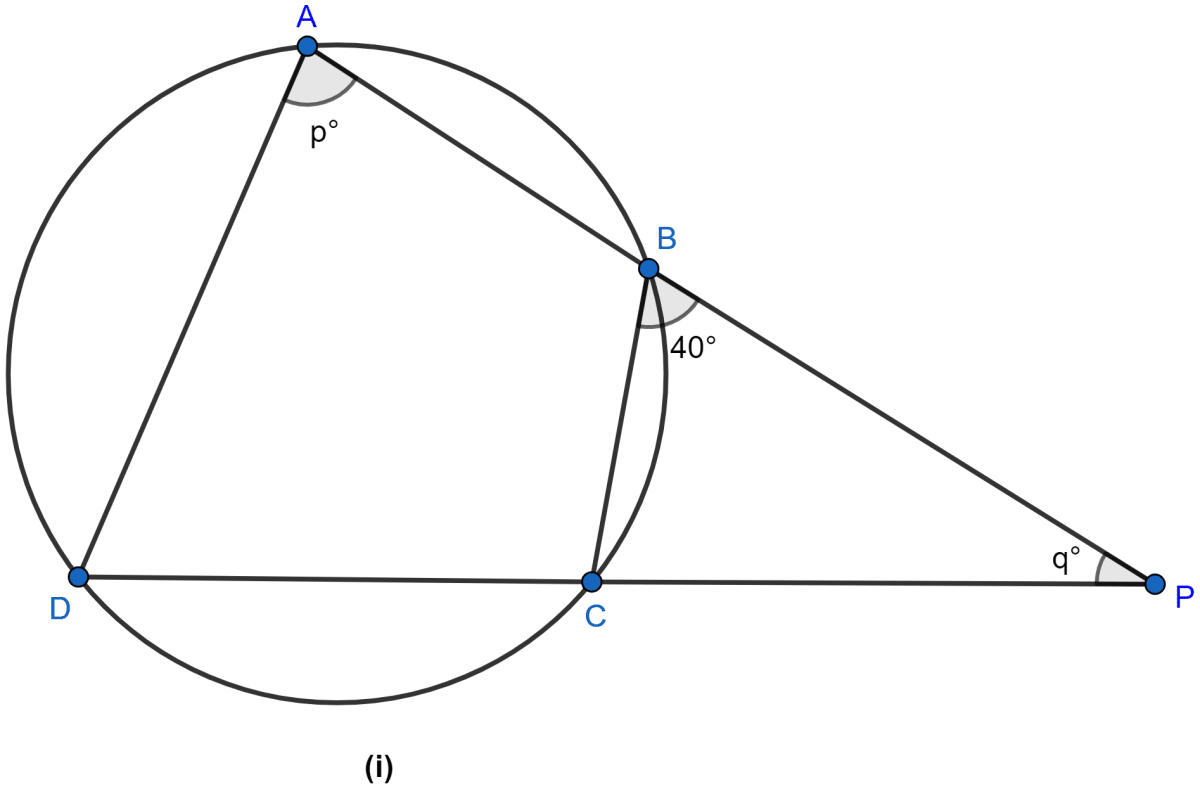
In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2q° and the points C, P, B and Q are concyclic, find the values of p and q.
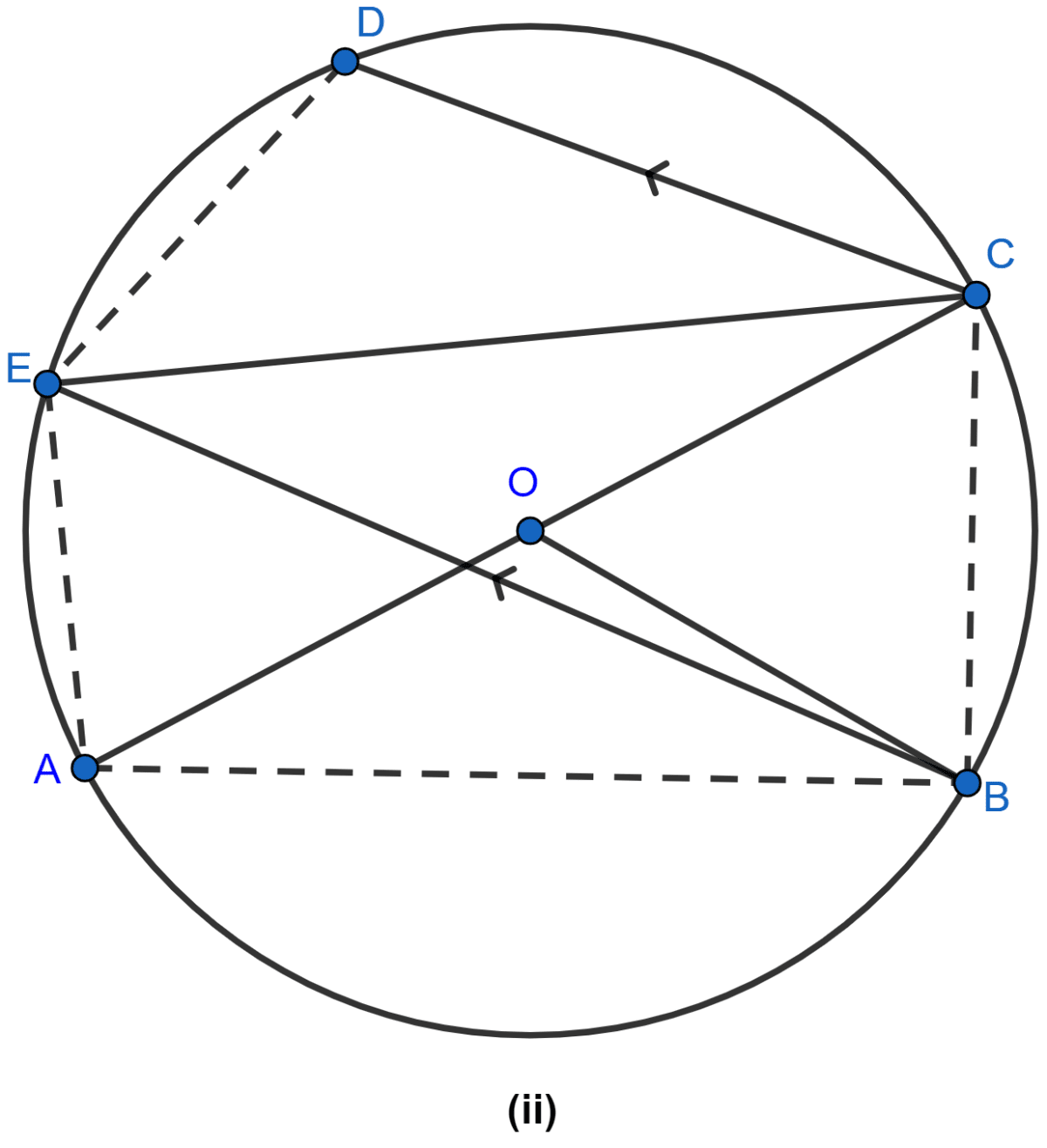
In the figure (ii) given below, AC is a diameter of the circle with centre O. If CD || BE, ∠AOB = 130° and ∠ACE = 20°, find :
(i) ∠BEC
(ii) ∠ACB
(iii) ∠BCD
(iv) ∠CED.
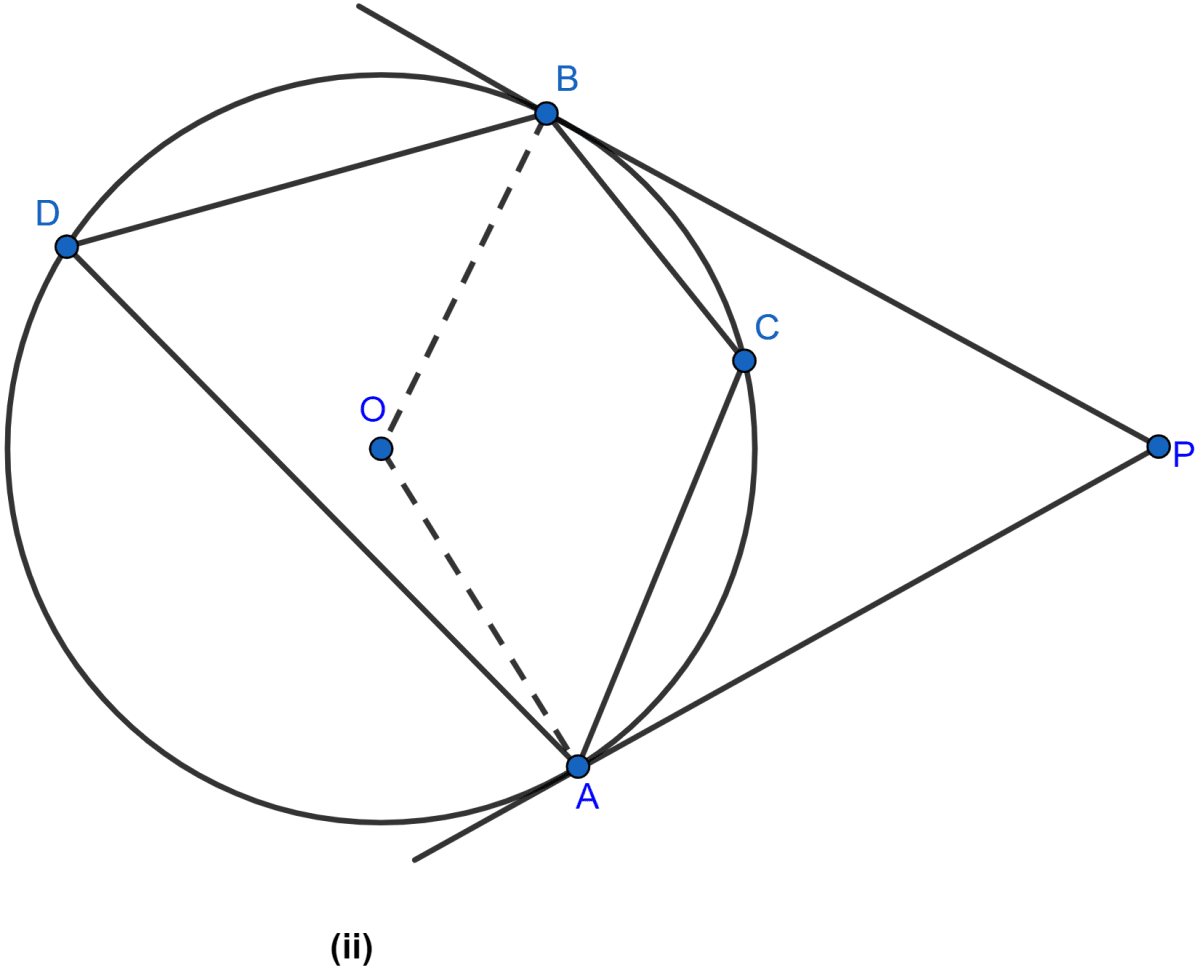
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find
(i) ∠ADB
(ii) ∠AOB
(iii) ∠ACB
(iv) ∠APB.