Mathematics
In the figure given, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°.
Calculate :
(i) ∠RNM,
(ii) ∠NRM.

Answer
(i) Join RN and MS.

∠RMS = 90° [Angle in a semi-circle is a right angle]
In ∆RMS
⇒ ∠RMS + ∠RSM + ∠MRS = 180° [Angle sum property of triangle]
⇒ 90° + ∠RSM + 29° = 180°
⇒ ∠RSM + 119° = 180°
⇒ ∠RSM = 180° - 119° = 61°.
Sum of opposite angles in a cyclic quadrilateral = 180°.
⇒ ∠RNM + ∠RSM = 180°
⇒ ∠RNM + 61° = 180°
⇒ ∠RNM = 180° - 61° = 119°.
Hence, ∠RNM = 119°.
(ii) Now as RS || NM,
∠NMR = ∠MRS = 29° [Alternate angles are equal]
From figure,
∠NMS = ∠NMR + ∠RMS = 29° + 90° = 119°.
Sum of opposite angles in a cyclic quadrilateral = 180°.
In quadrilateral NMSR,
⇒ ∠NRS + ∠NMS = 180°
⇒ ∠NRM + ∠MRS + ∠NMS = 180°
⇒ ∠NRM + 29° + 119° = 180°
⇒ ∠NRM = 180° - 119° - 29°
⇒ ∠NRM = 32°.
Hence, ∠NRM = 32°.
Related Questions
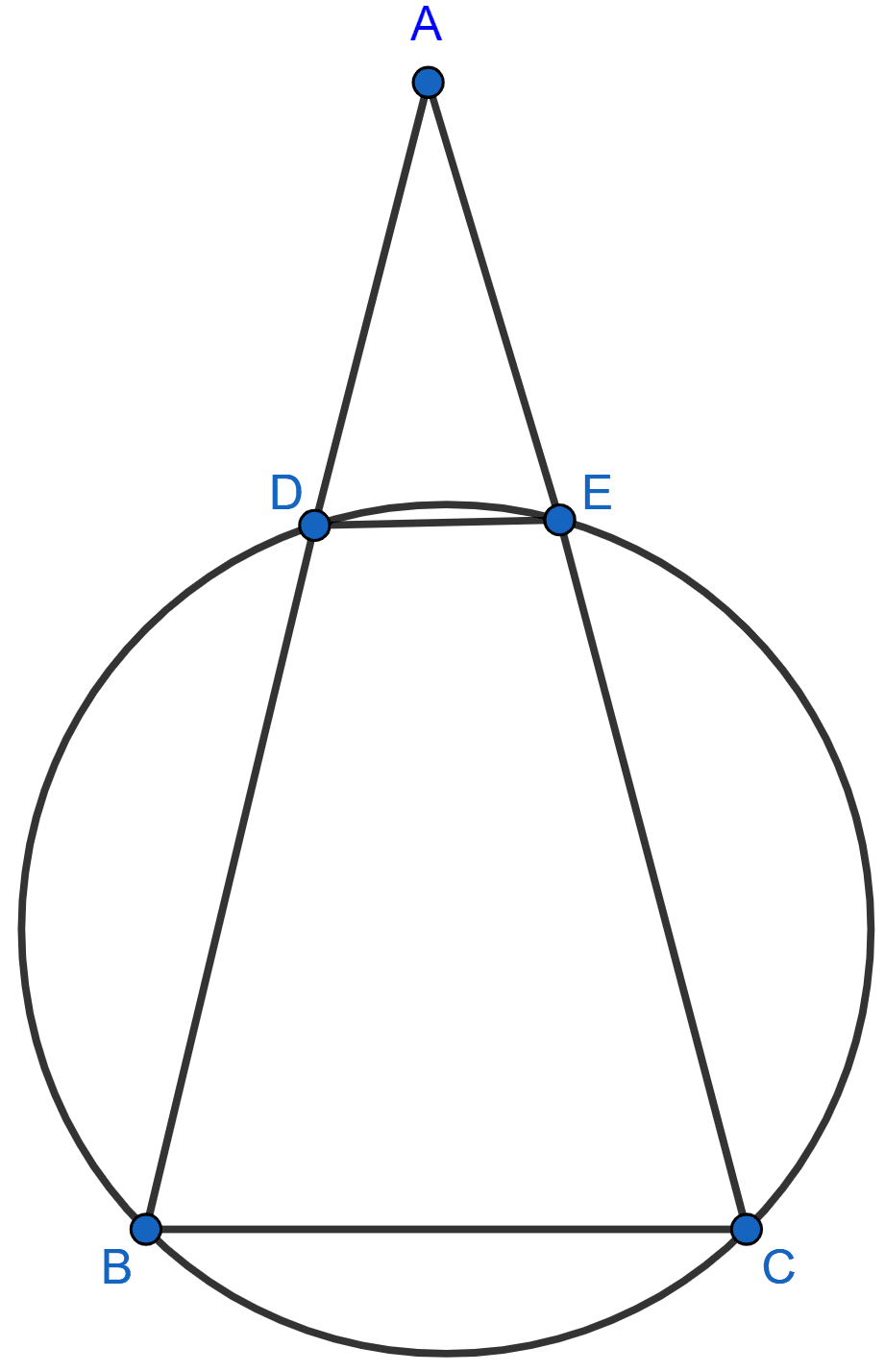
The figure given below, shows a circle with centre O.
Given : ∠AOC = a and ∠ABC = b.
(i) Find the relationship between a and b.
(ii) Find the measure of angle OAB, if OABC is a parallelogram.
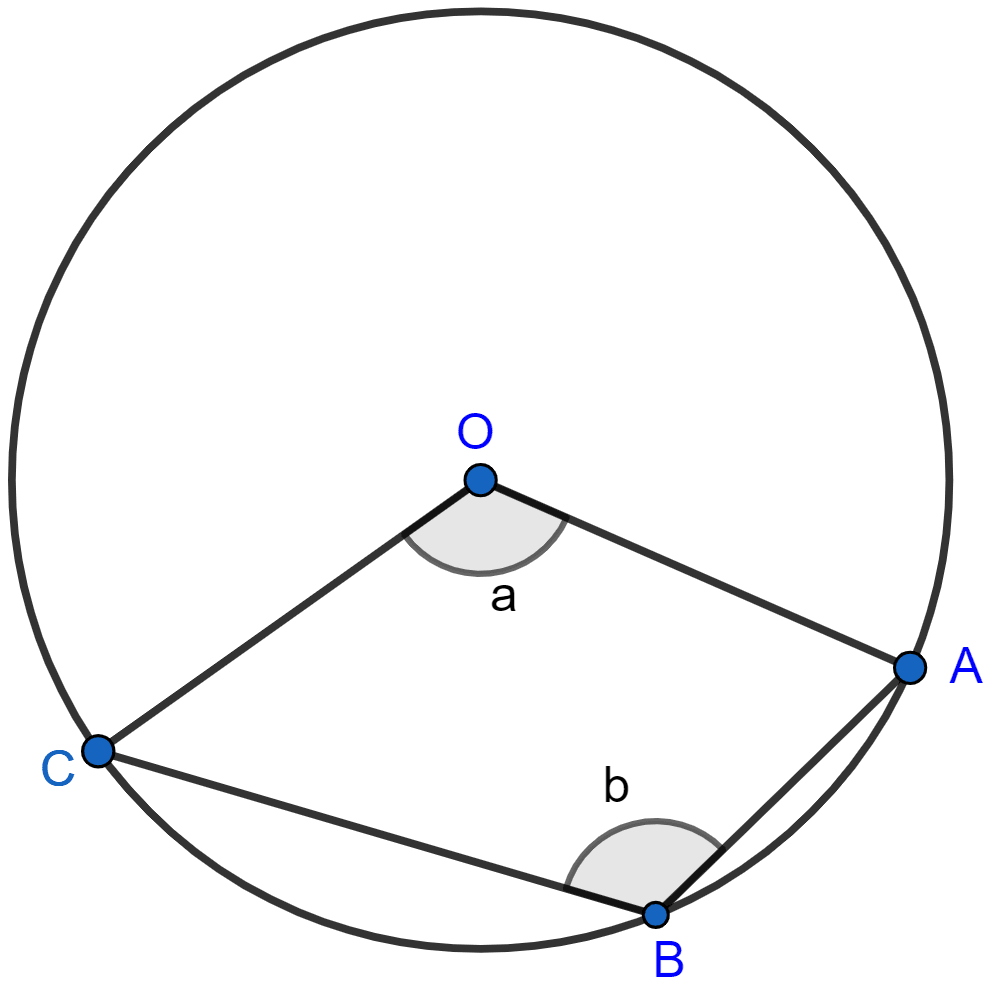
In the given figure, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that :
SQ = SR.
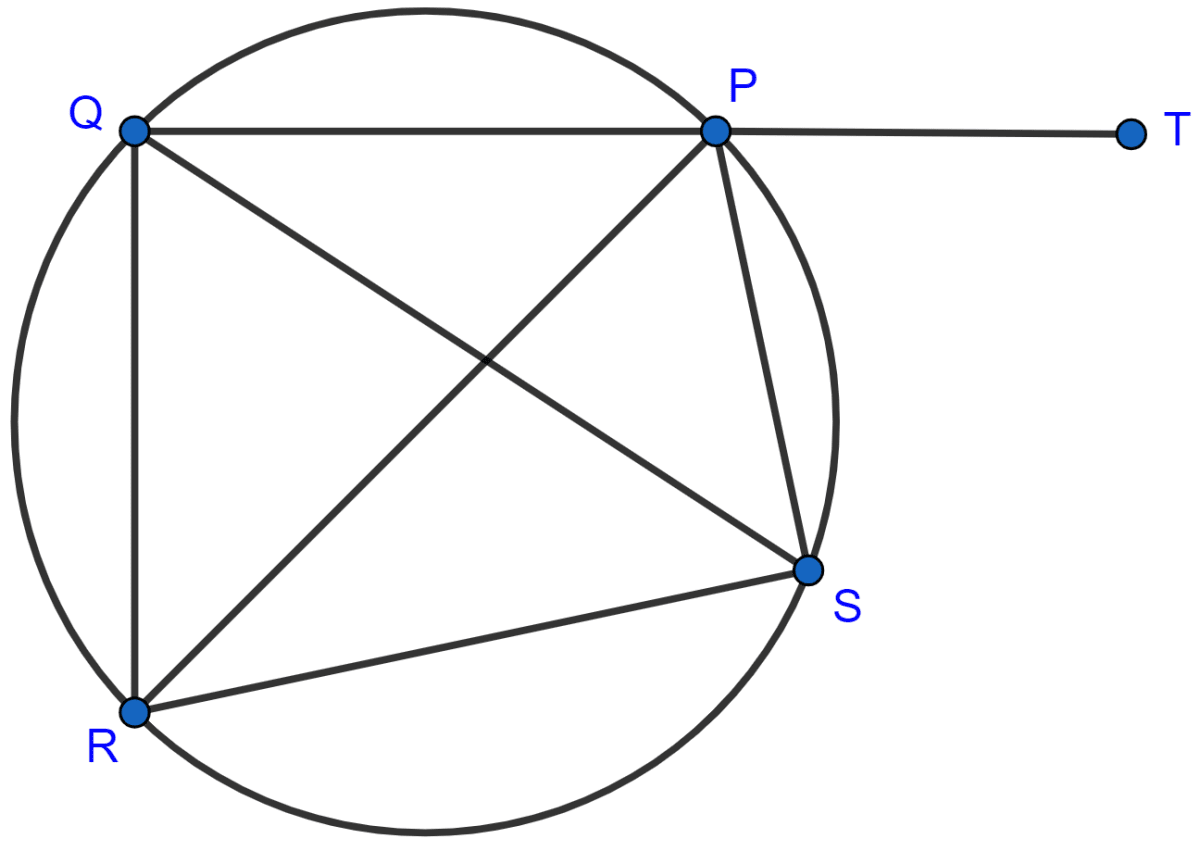
In the figure, O is the center of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
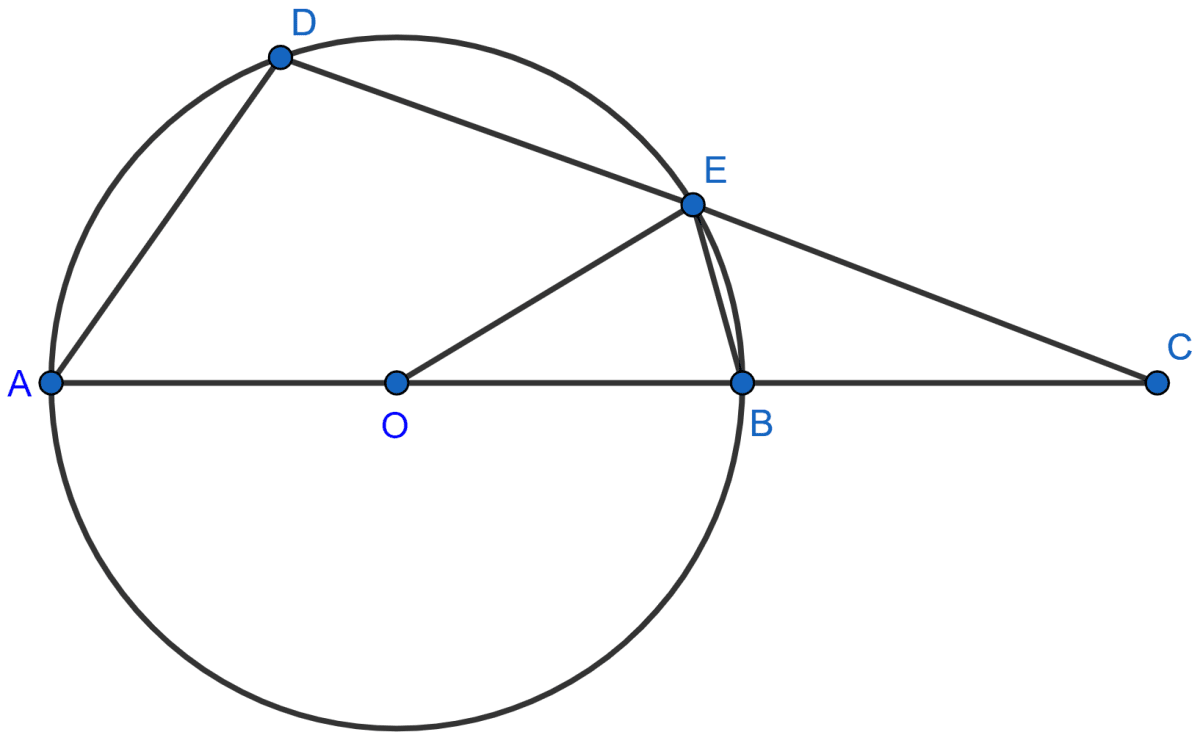
In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.