Mathematics
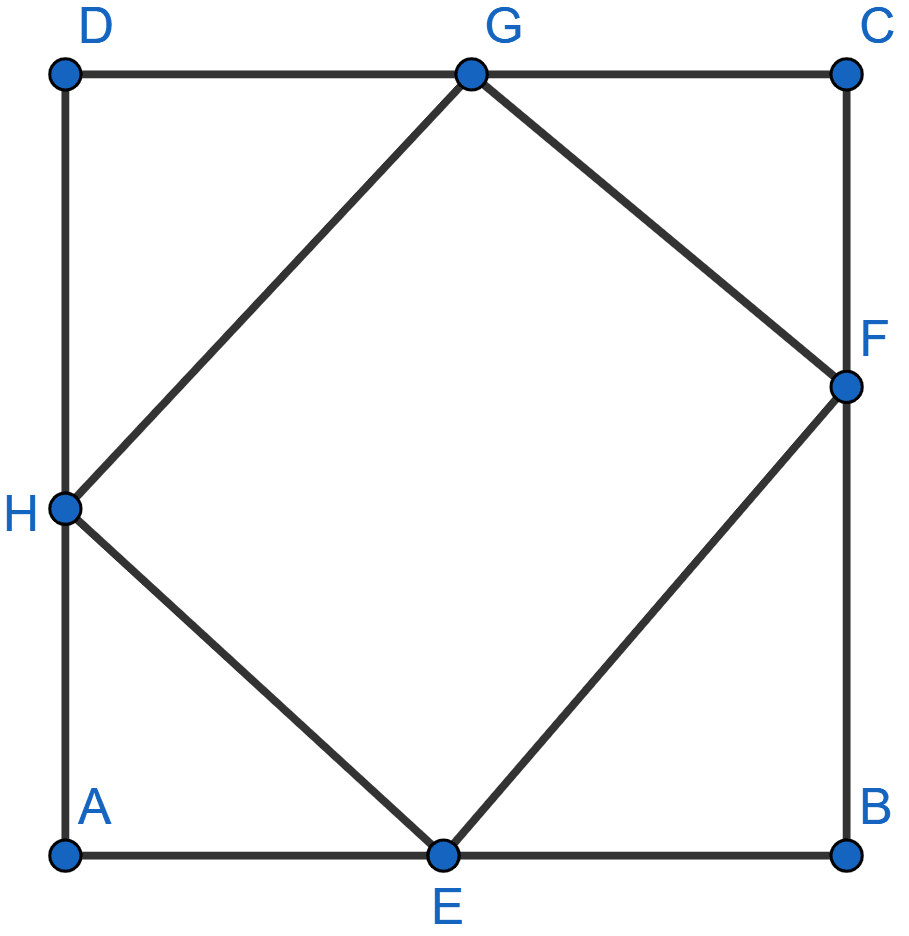
In the figure given below, ABCD is a square of side 7 cm. If
AE = FC = CG = HA = 3 cm,
(i) prove that EFGH is a rectangle.
(ii) find the area and perimeter of EFGH.
Pythagoras Theorem
40 Likes
Answer
(i) Given, ABCD is a square of side 7 cm and AE = FC = CG = HA = 3 cm.
From figure,
DH = DA - HA = 7 - 3 = 4 cm,
GD = DC - CG = 7 - 3 = 4 cm,
EB = AB - AE = 7 - 3 = 4 cm,
FB = BC - FC = 7 - 3 = 4 cm.
Since in square, sides are perpendicular to each other,
By pythagoras theorem,
In right angle triangle HAE,
⇒ HE2 = HA2 + AE2
⇒ HE2 = 32 + 32
⇒ HE2 = 9 + 9
⇒ HE2 = 18
⇒ HE = cm.
In right angle triangle FCG,
⇒ GF2 = GC2 + FC2
⇒ GF2 = 32 + 32
⇒ GF2 = 9 + 9
⇒ GF2 = 18
⇒ GF = cm.
In right angle triangle GDH,
⇒ GH2 = GD2 + DH2
⇒ GH2 = 42 + 42
⇒ GH2 = 16 + 16
⇒ GH2 = 32
⇒ GH = cm.
In right angle triangle EBF,
⇒ EF2 = EB2 + FB2
⇒ EF2 = 42 + 42
⇒ EF2 = 16 + 16
⇒ EF2 = 32
⇒ EF = cm.
In isosceles triangle AEH,
∠E = ∠H = x (let) (As angles opposite to equal side in isosceles triangle are equal).
So, ∠A + ∠E + ∠H = 180°
90° + x + x = 180°
2x = 90°
x = 45°
Similar is the case for triangles EBF, GDH, FCG.
From figure,
∠AEH + ∠HEF + ∠FEB = 180° (Linear pairs)
45° + ∠HEF + 45° = 180°
∠HEF = 90°
Since, angles of EFGH = 90° and EH = GF and HG = EF.
Hence, proved that EFGH is a rectangle.
(ii) Area of EFGH = EF × GF = = 24 cm2.
Perimeter of EFGH = 2(EF + GF) = cm.
Hence, area = 24 cm2 and perimeter = cm.
Answered By
24 Likes
Related Questions
In figure given below, AB || DC, BC = AD = 13 cm, AB = 22 cm and DC = 12 cm. Calculate the height of the trapezium ABCD.

In figure given below, AB || DC, ∠A = 90°, DC = 7 cm, AB = 17 cm and AC = 25 cm. Calculate BC.

AD is perpendicular to the side BC of an equilateral △ABC. Prove that 4AD2 = 3AB2.
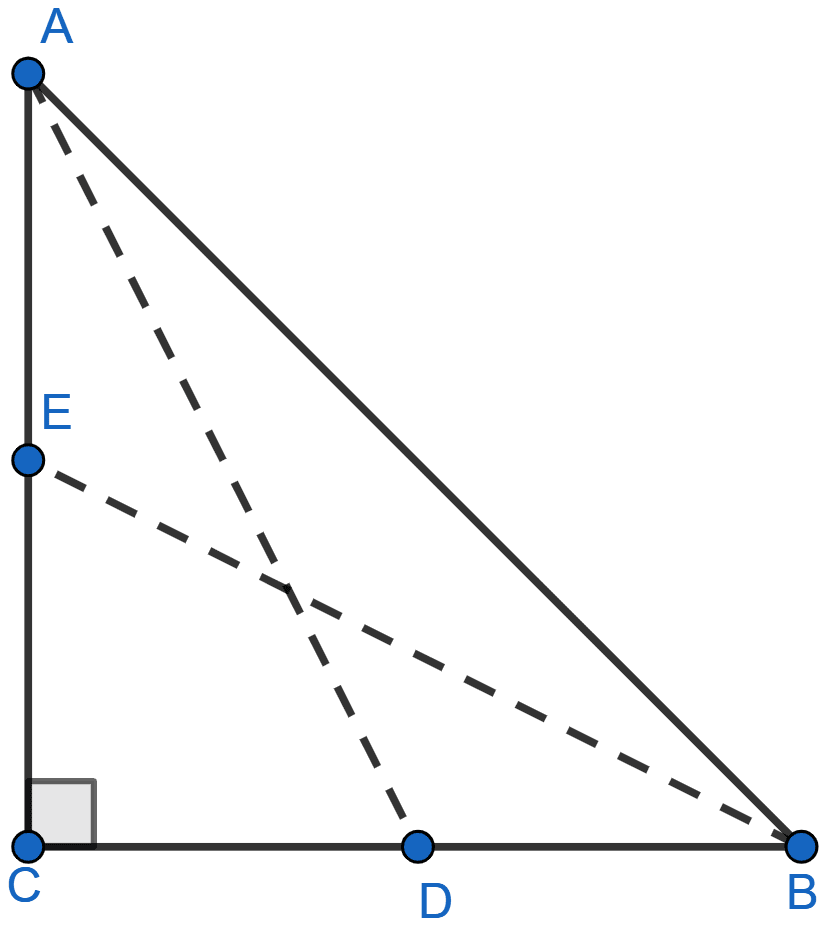
In the adjoining figure, D and E are mid-points of the sides BC and CA respectively of a △ABC, right angled at C. Prove that :
(i) 4AD2 = 4AC2 + BC2
(ii) 4BE2 = 4BC2 + AC2
(iii) 4(AD2 + BE2) = 5AB2