Mathematics
In the figure given alongside, AOB is a diameter of the circle and ∠AOC = 110°, find ∠BDC.

Circles
28 Likes
Answer
Join AD.

We know that,
Angle at the center is double the angle at the circumference subtended by the same chord.
∠ADC = ∠AOC = x 110° = 55°.
Also, we know that
Angle in the semi-circle is a right angle.
∠ADB = 90°
From figure,
∠BDC = ∠BDA - ∠ADC = 90° - 55° = 35°.
Hence, ∠BDC = 35°.
Answered By
21 Likes
Related Questions
Calculate:
(i) ∠CDB,
(ii) ∠ABC,
(iii) ∠ACB.
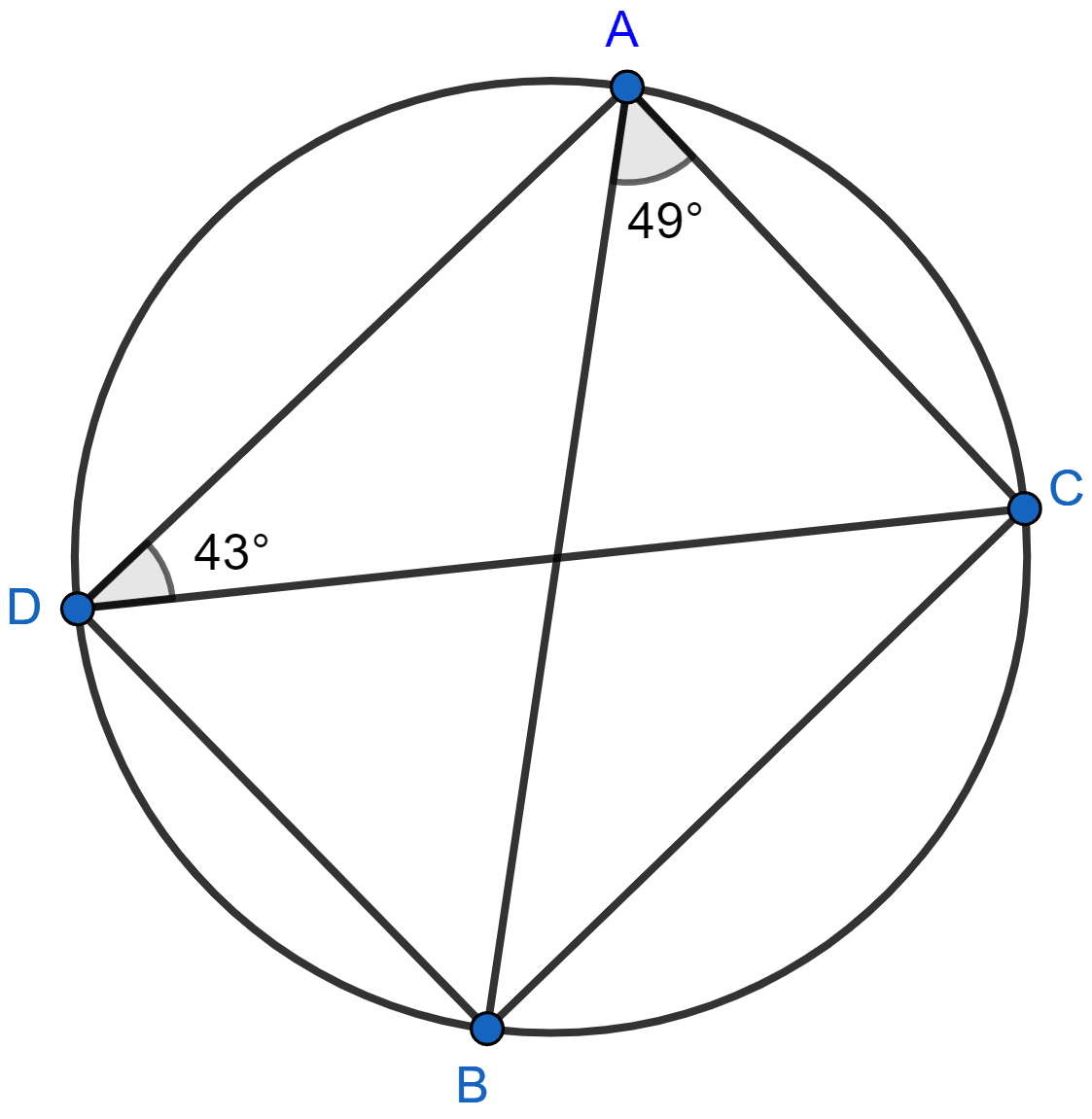
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.

In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.
