Mathematics
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

Circles
23 Likes
Answer
We know that,
Angle at the centre is double the angle at the circumference subtended by the same chord.
∠ACB = ∠AOB = = 30°.
In △BDC,
⇒ ∠BDC + ∠DCB + ∠CBD = 180° [Angle sum property]
⇒ 100° + 30° + ∠CBD = 180° [From figure, ∠DCB = ∠ACB]
⇒ ∠CBD + 130° = 180°
⇒ ∠CBD = 180° - 130° = 50°.
From figure,
⇒ ∠OBC = ∠CBD = 50°.
Hence, ∠OBC = 50°.
Answered By
13 Likes
Related Questions
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.

In the figure given alongside, AOB is a diameter of the circle and ∠AOC = 110°, find ∠BDC.

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.

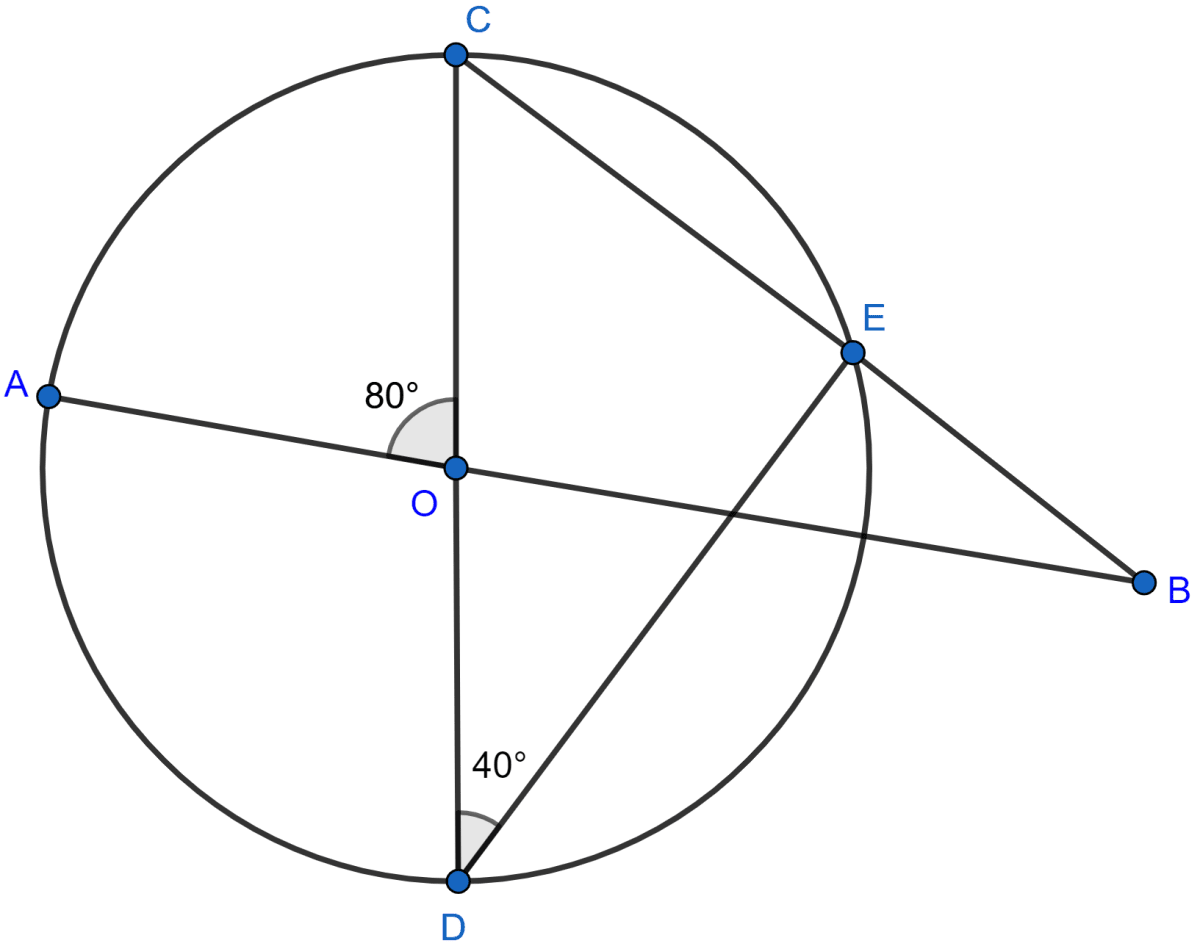
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in :
(i) ∠DCE,
(ii) ∠ABC.