Mathematics
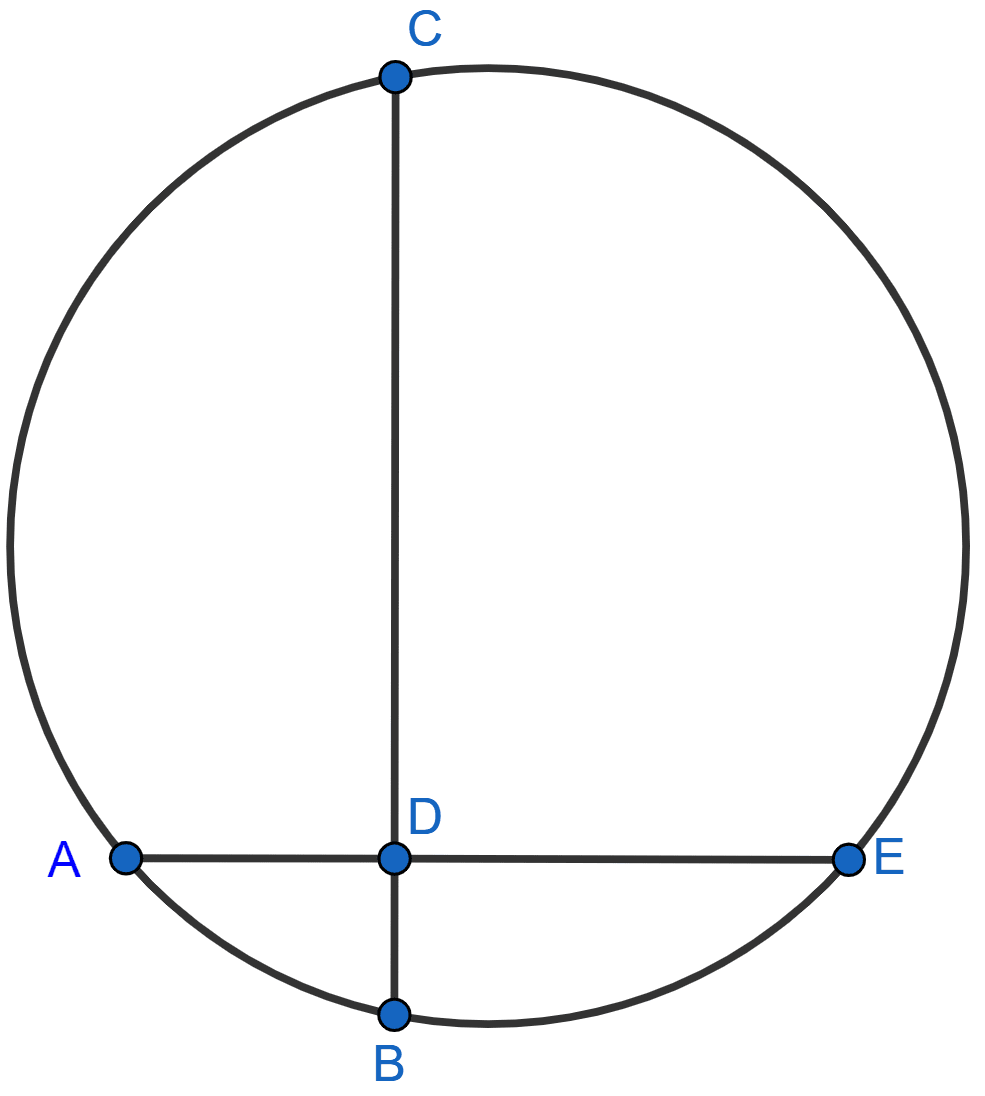
In the figure, chords AE and BC intersect each other at point D.
(i) If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.
(ii) If AD = BD, show that : AE = BC.
Circles
8 Likes
Answer
(i) Join AB.
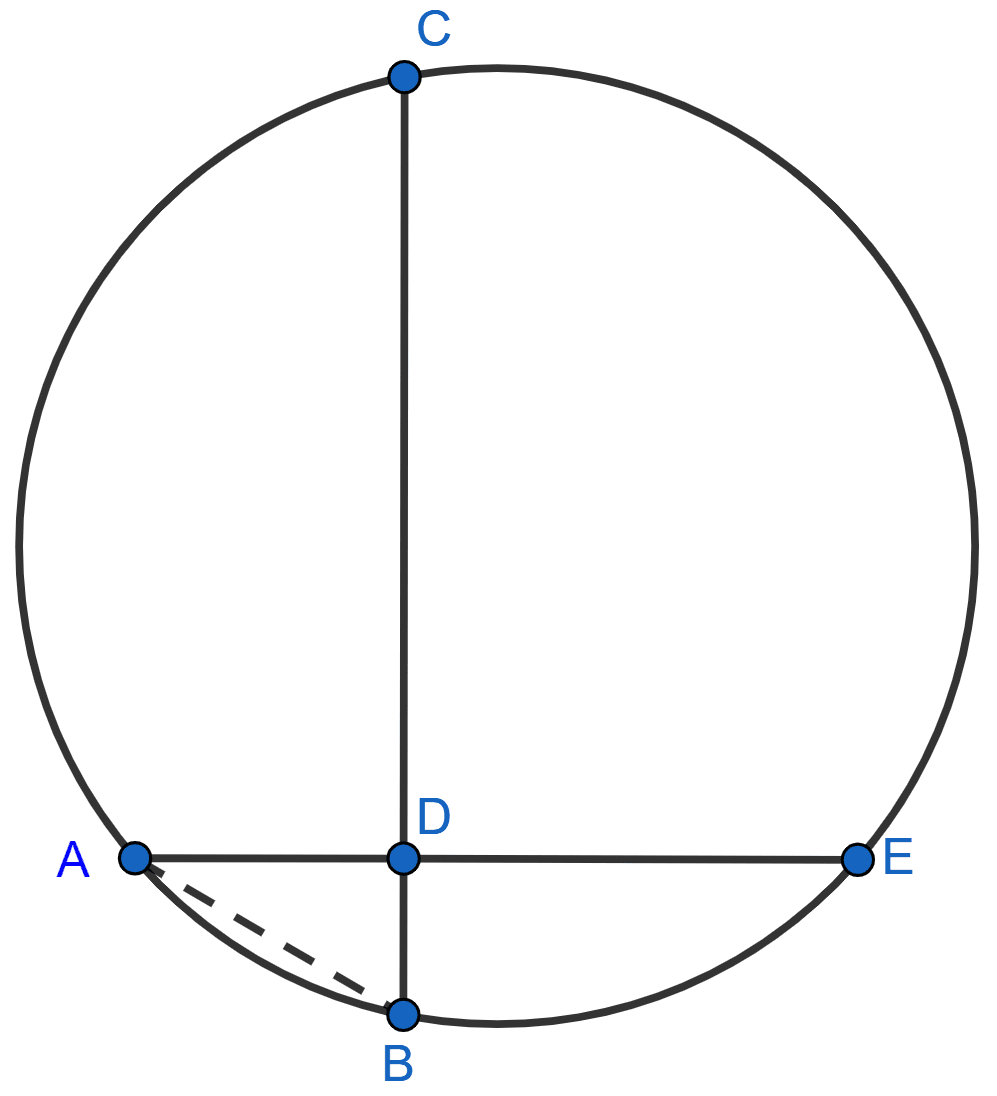
∠ADB = ∠CDE = 90° [Vertically opposite angles are equal.]
In right angle triangle ADB,
⇒ AB2 = AD2 + BD2
⇒ 52 = AD2 + 42
⇒ 25 = AD2 + 16
⇒ AD2 = 25 - 16
⇒ AD2 = 9
⇒ AD =
⇒ AD = 3 cm.
We know that,
If two chords of a circle intersect internally or externally then the product of the lengths of their segment is equal.
From figure,
Chords AE and CB intersect internally at point D.
⇒ AD × DE = CD × BD
⇒ 3 × DE = 4 × 9
⇒ DE =
⇒ DE = 12 cm.
Hence, DE = 12 cm.
(ii) Given,
AD = BD ……..(1)
AD = BD = x (let)
We know that,
⇒ AD × DE = CD × BD
⇒ (x)DE = (x)CD
⇒ DE = CD ……….(2)
Adding (1) and (2), we get :
⇒ AD + DE = BD + CD
⇒ AE = BC.
Hence, proved that AE = BC.
Answered By
7 Likes
Related Questions
Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
![In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that ∠CAD = 1/2 [∠PBA - ∠PAB]. Tangents and Intersecting Chords, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q13-c18-ex-18-b-tangents-concise-maths-solutions-icse-class-10-1200x843.png)
In the adjoining figure, O is the center of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.

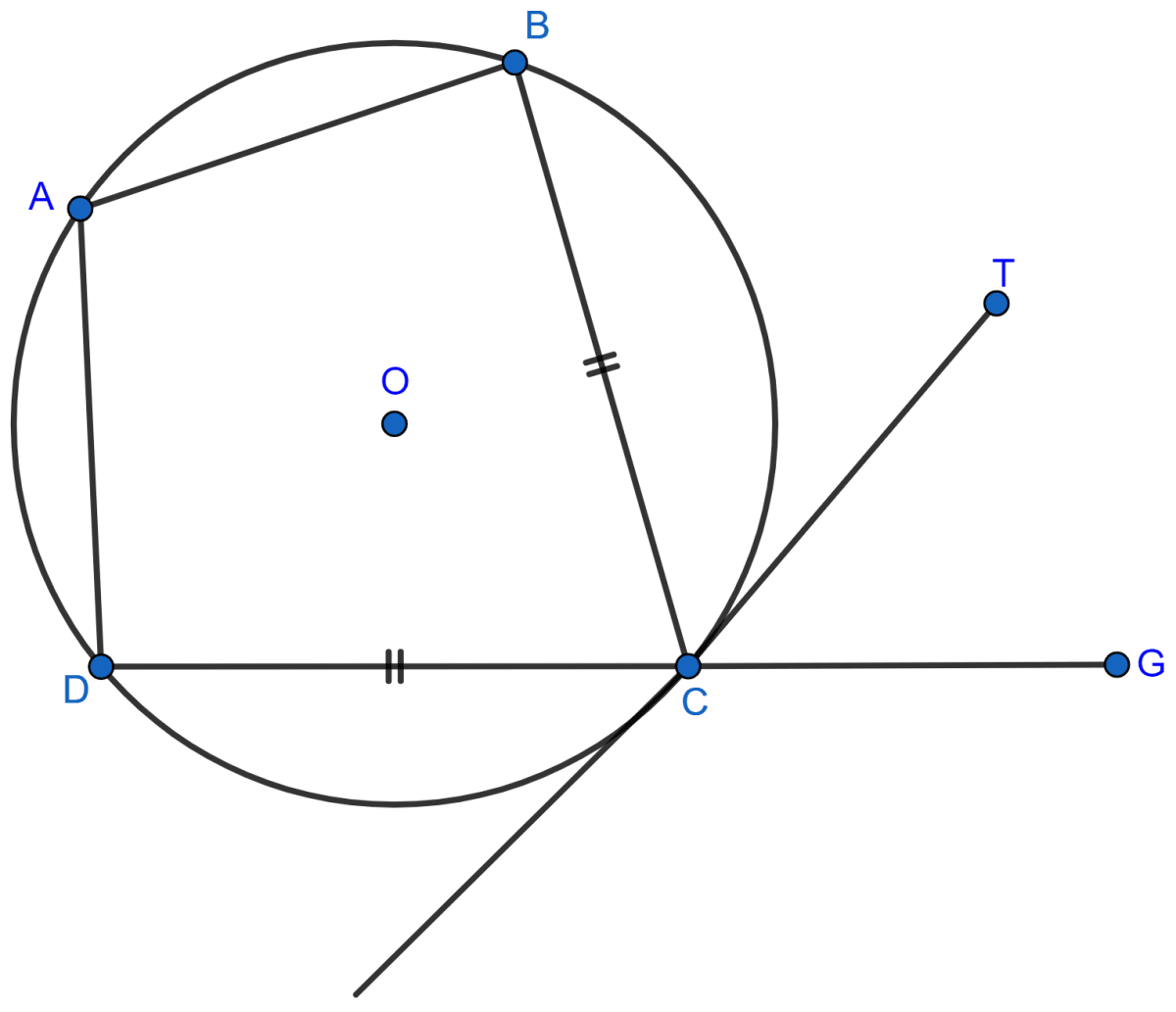
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the center of the circle, find :
(i) angle BCT
(ii) angle DOC
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that :
∠CAD = [∠PBA - ∠PAB]
![In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that ∠CAD = 1/2 [∠PBA - ∠PAB]. Tangents and Intersecting Chords, Concise Mathematics Solutions ICSE Class 10.](https://cdn1.knowledgeboat.com/img/cm10/q12-c18-ex-18-b-tangents-concise-maths-solutions-icse-class-10-1200x800.png)