Mathematics
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and O2 are the centers of two circles.

Circles
4 Likes
Answer
We know that,
Angle in a semi-circle is a right angle.
∴ ∠DBA = ∠CBA = 90°
Adding both we get,
⇒ ∠DBA + ∠CBA = 180°
Hence proved that, D, B and C form a straight line.
Answered By
2 Likes
Related Questions
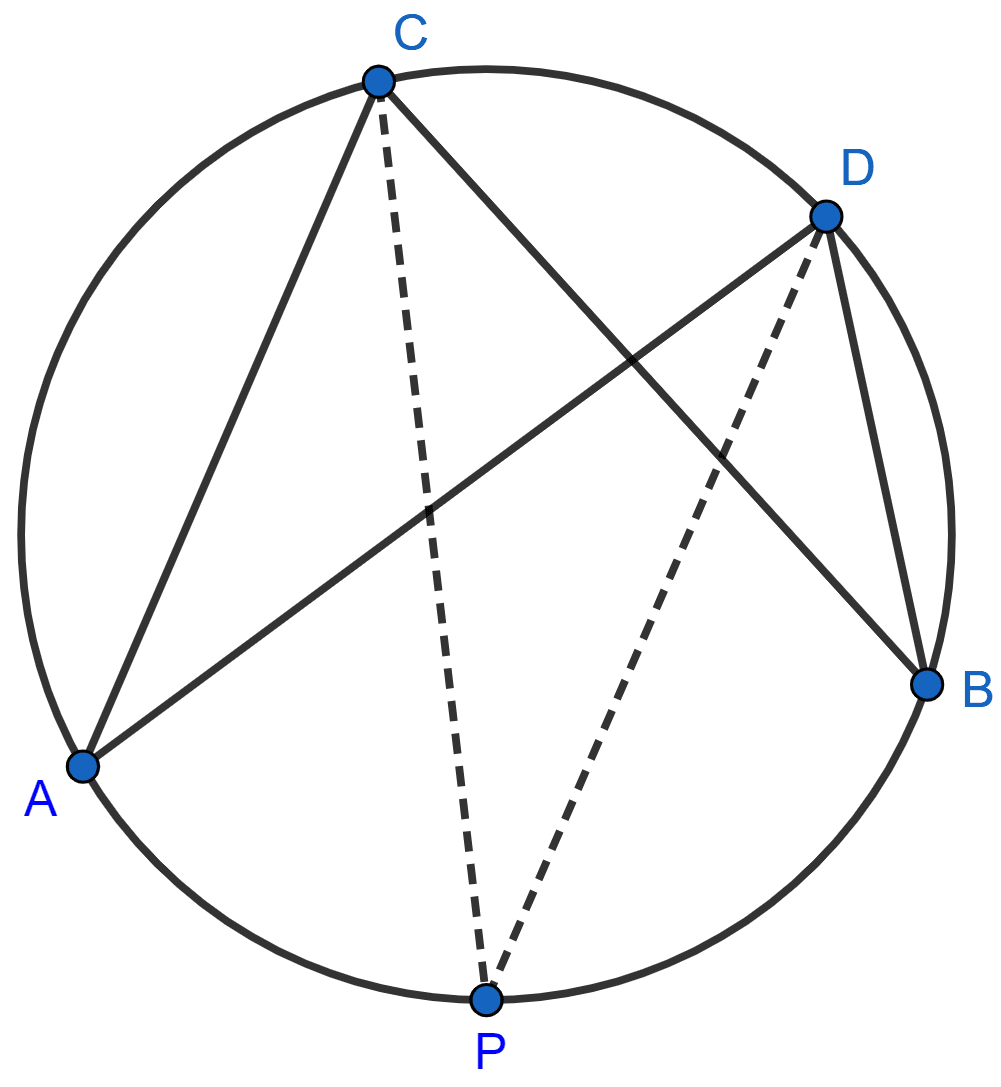
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD