Mathematics
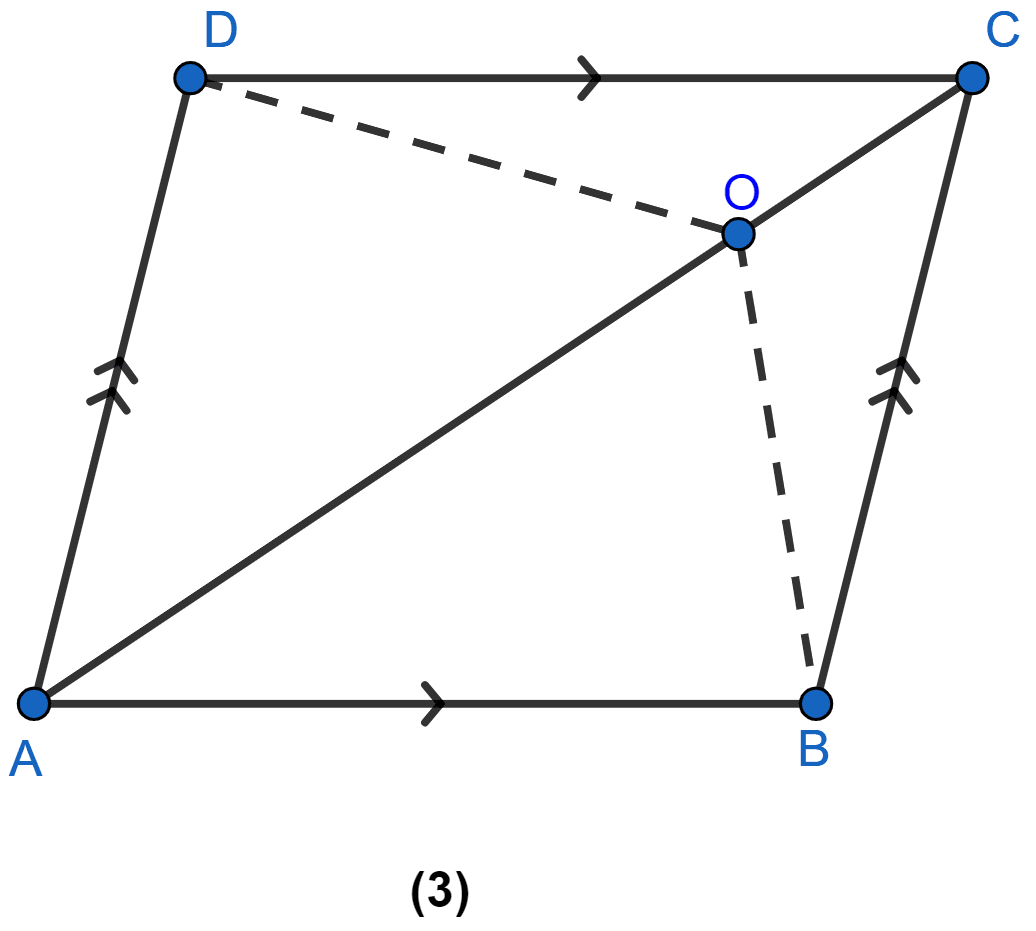
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.
Answer
Join BD, which meets AC at P.
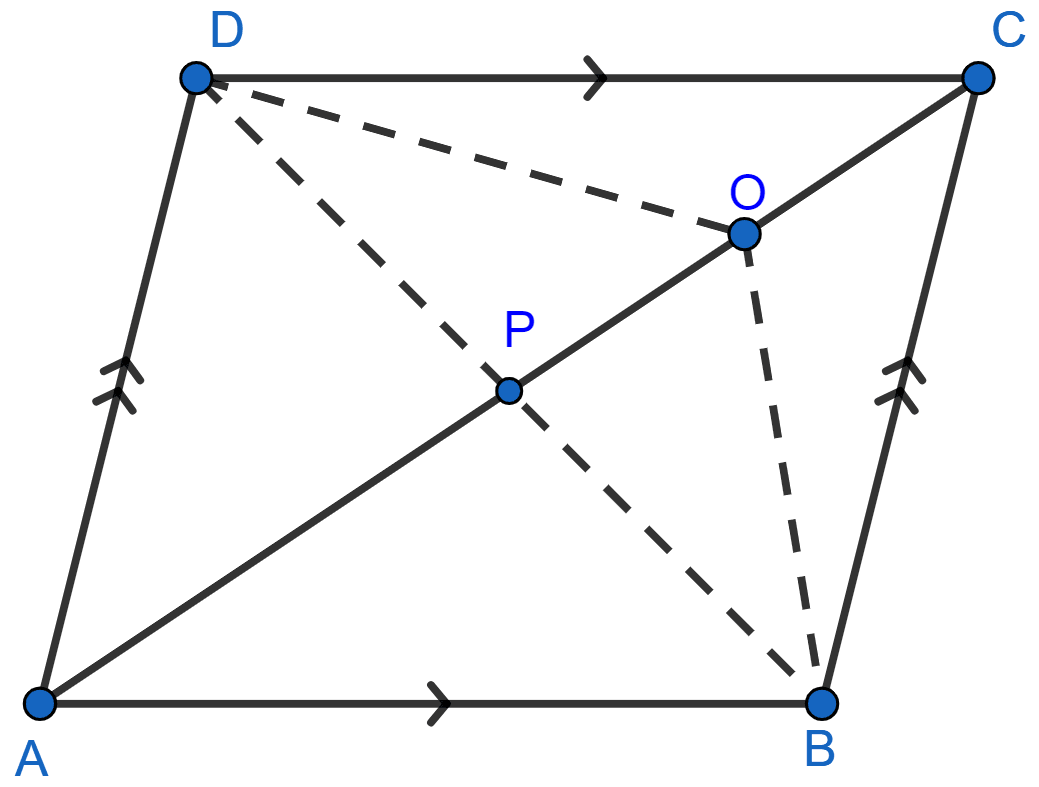
In ∆ABD, AP is the median (As P is mid-point of BD because diagonals of || gm bisect each other).
Since, median of triangle divides it into two triangles of equal area.
∴ Area of ∆ABP = Area of ∆ADP …….(i)
Similarly,
PO is median of ∆BOD,
∴ Area of ∆BOP = Area of ∆POD …….(ii)
Now, adding (i) and (ii), and we get
⇒ Area of ∆ABP + Area of ∆BOP = Area of ∆ADP + Area of ∆POD
⇒ Area of ∆AOB = Area of ∆AOD.
Hence, proved that area of ∆AOB = area of ∆AOD.
Related Questions
In figure (2) given below, DE is drawn parallel to the diagonal AC of the quadrilateral ABCD to meet BC produced at point E. Prove that area of quad. ABCD = area of ∆ABE.

In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
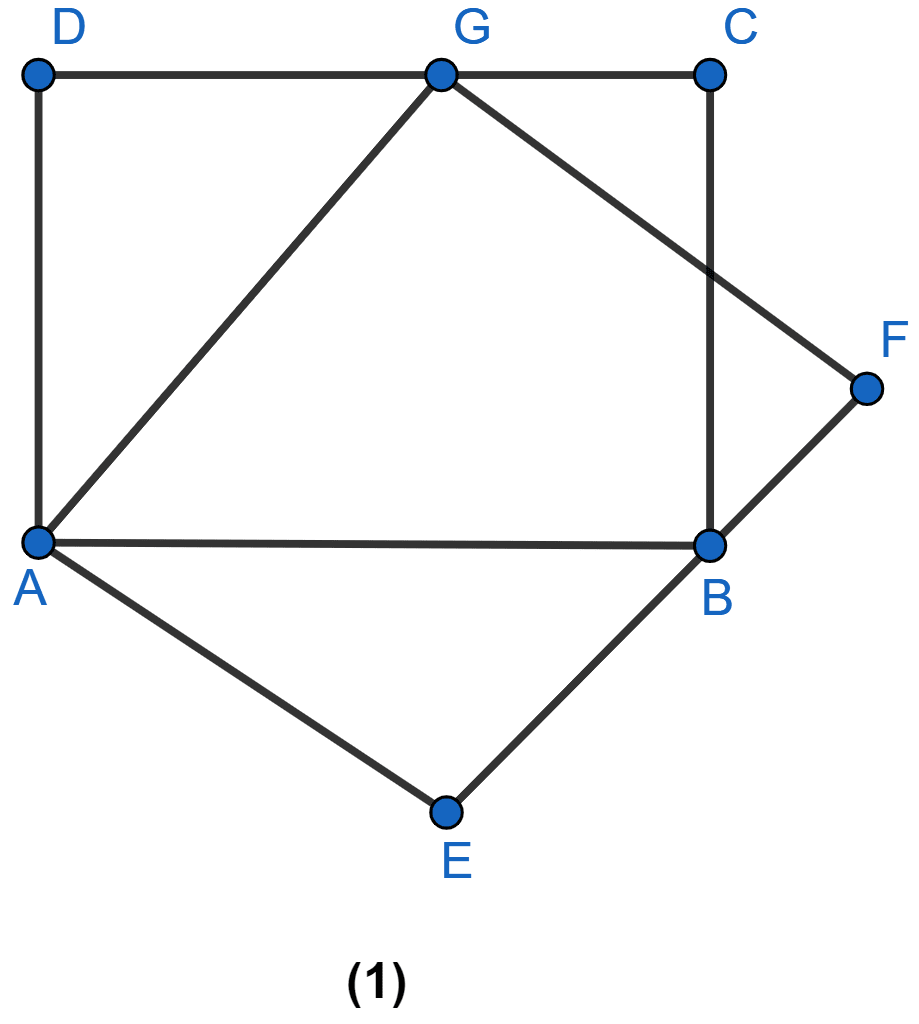
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.