Mathematics
Answer
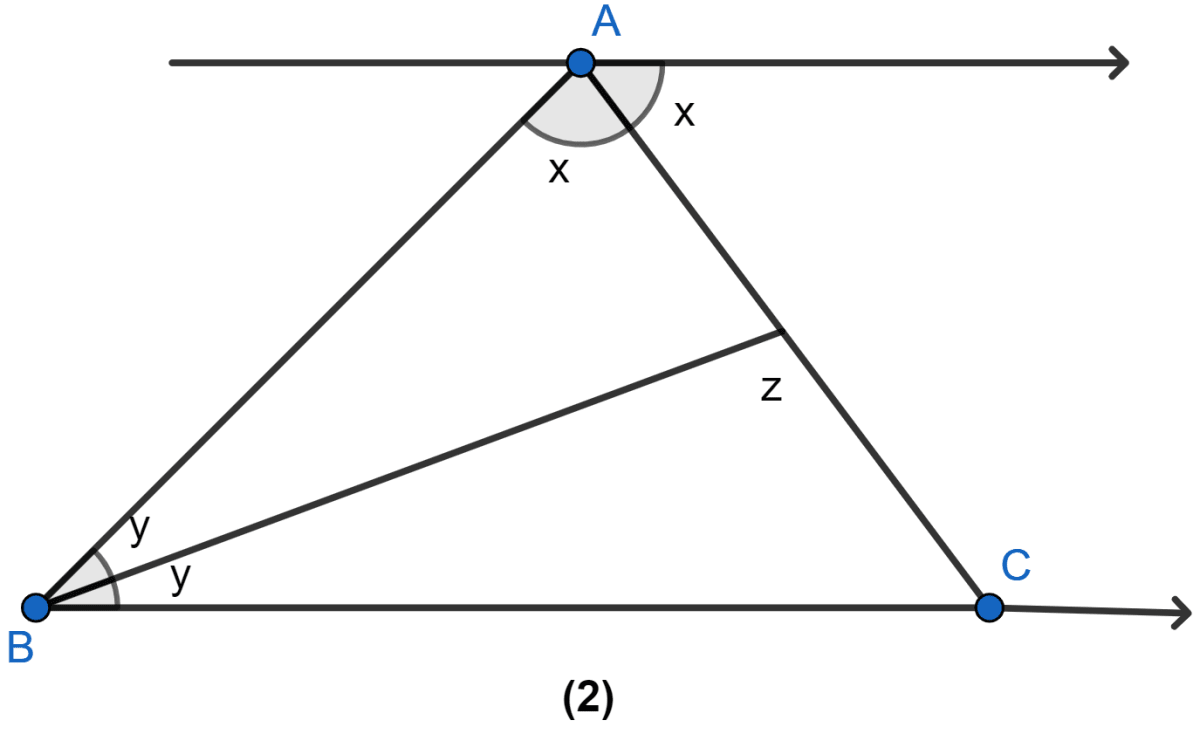
(i) From figure,
∠ACB = x (Alternate angles)
In △ABC,
⇒ x + (y + y) + ∠ACB = 180°
⇒ x + 2y + x = 180°
⇒ 2x + 2y = 180°
⇒ x + y = 90°.
Hence, proved that x + y = 90°.
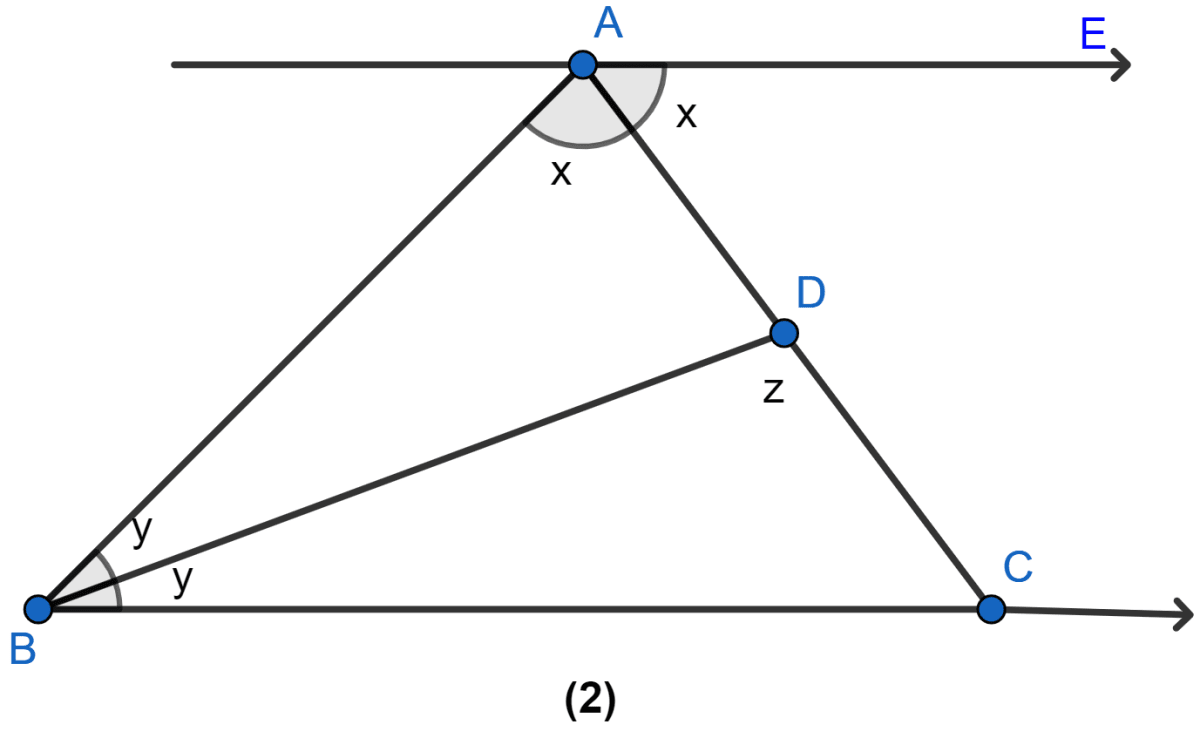
(ii) Now in △BCD,
⇒ y + z + ∠BCD = 180° (Sum of all angles in a triangle is 180°)
⇒ y + z + x = 180°
⇒ 90° + z = 180° [∵ x + y = 90°]
⇒ z = 90°.
Hence, proved that z = 90°.
(iii) In △ABC,
∠ACB = ∠BAC = x
∴ AB = BC (As sides opposite to equal angles are equal.)
Hence, proved that AB = BC.
Related Questions
In the figure (3) given below, calculate the size of each lettered angle.

In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that
(i) AC > DC
(ii) AB > AD.

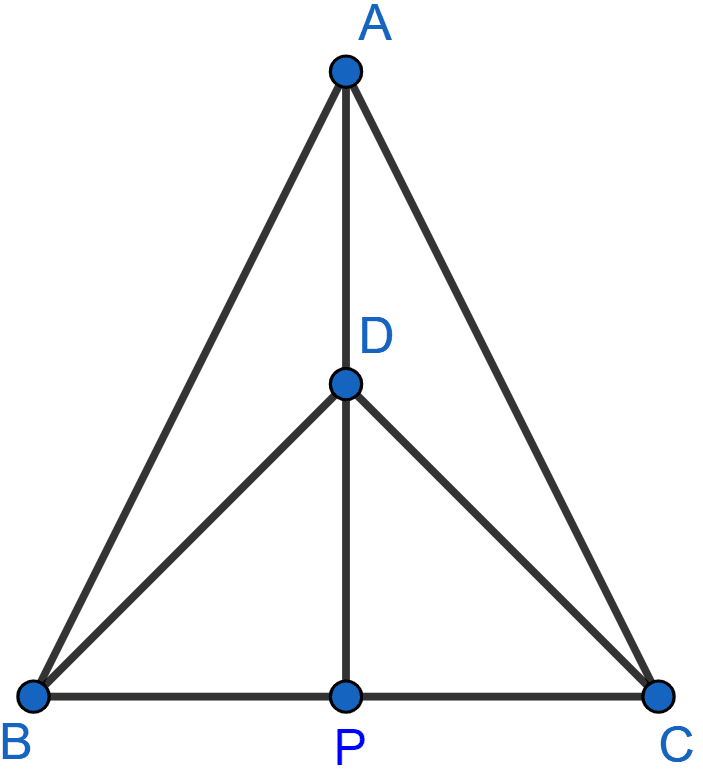
In the adjoining figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
In the adjoining figure, AP ⊥ l and PR > PQ. Show that AR > AQ.