Mathematics
In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that
(i) AC > DC
(ii) AB > AD.

Triangles
16 Likes
Answer
From figure,
∠DAC = ∠ACD = 35° (As angles opposite to equal sides are equal.)
∠ADC = 180° - (35° + 35°) = 180° - 70° = 110°.
Since, ∠ADC > ∠DAC
∴ AC > DC (Side opposite to greater angle is greater.)
Hence, proved that AC > DC.
(ii) From figure,
∠ADB = 180° - ∠ADC = 180° - 110° = 70°.
Considering △ABD,
AD = BD.
∴ ∠BAD = ∠ABD = a.
⇒ a + a + ∠ADB = 180°
⇒ 2a + 70° = 180°
⇒ 2a = 110°
⇒ a = 55°.
Since, ∠ADB > ∠ABD
∴ AB > AD. (Side opposite to greater angle is greater.)
Hence, proved that AB > AD.
Answered By
9 Likes
Related Questions
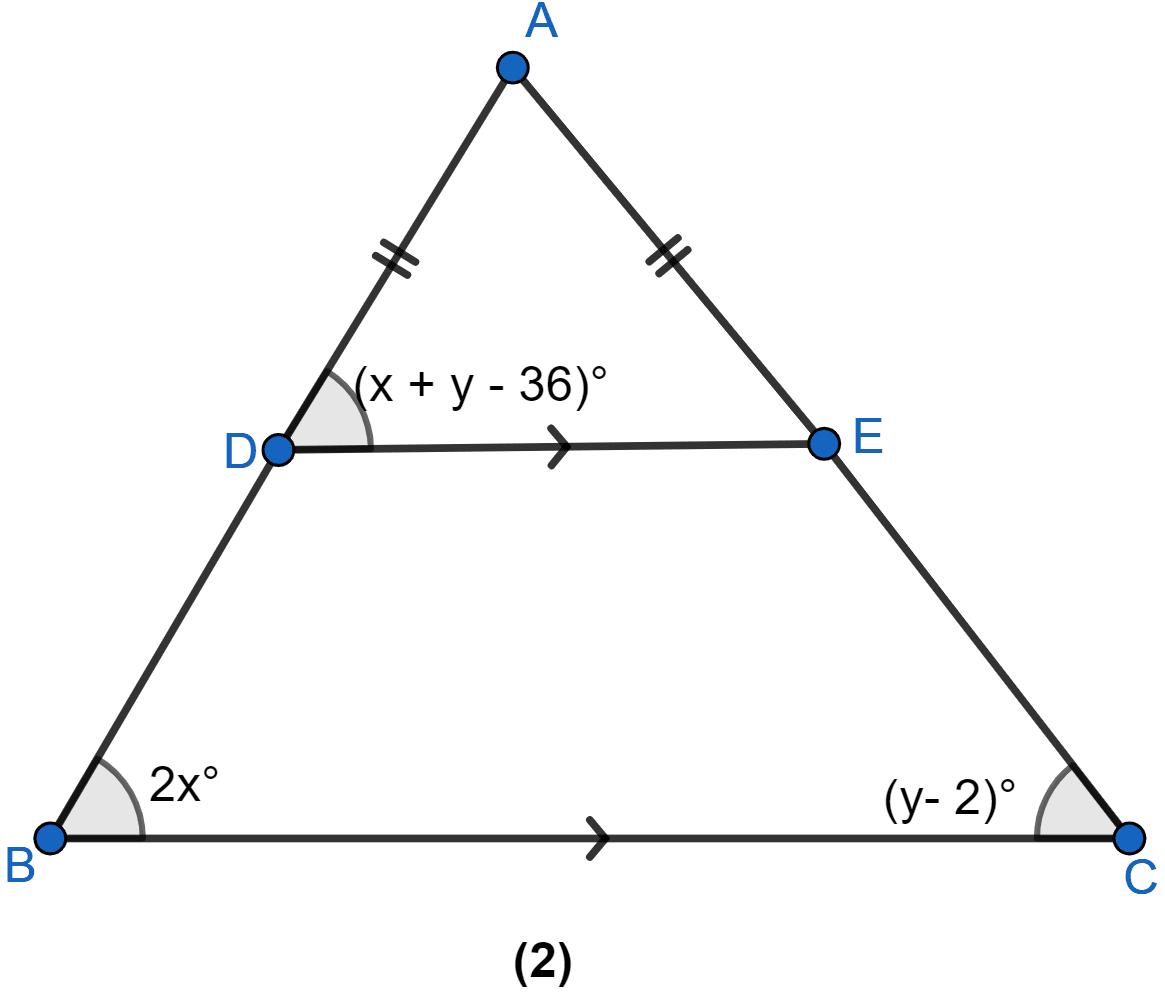
In the figure (2) given below, AB = AC and DE || BC. Calculate
(i) x
(ii) y
(iii) ∠BAC
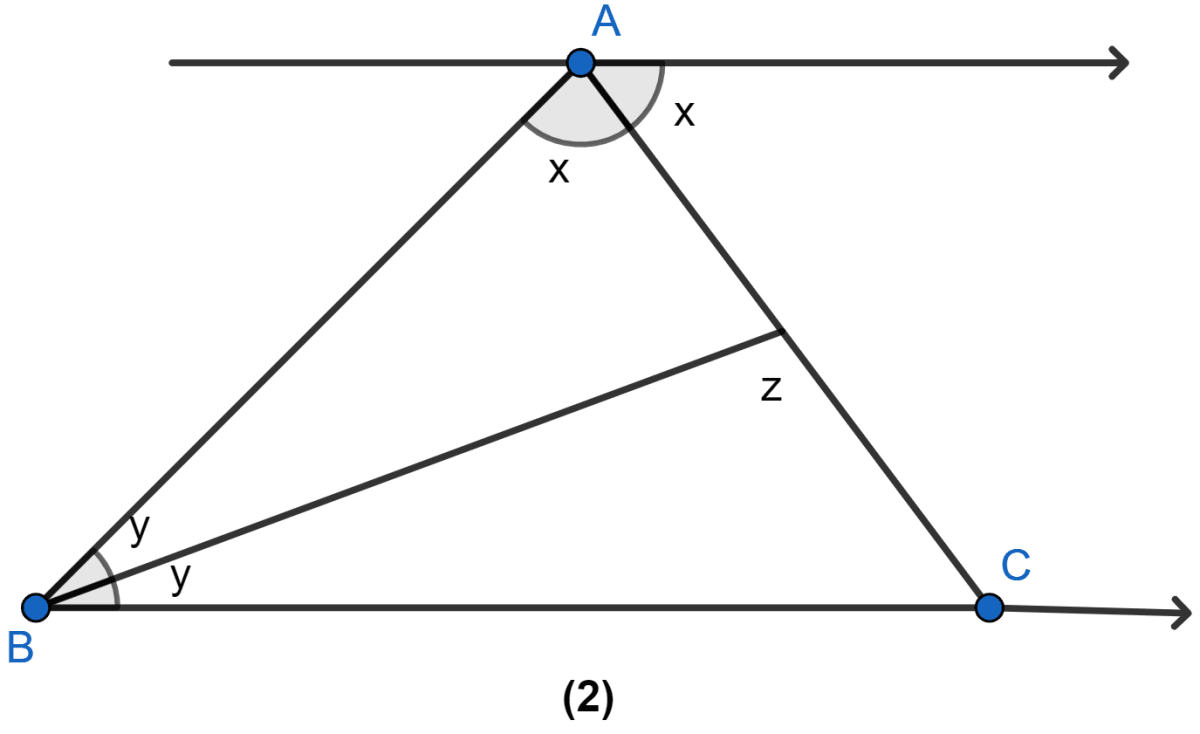
In the figure (3) given below, calculate the size of each lettered angle.

In the figure (2) given below, prove that
(i) x + y = 90°
(ii) z = 90°
(iii) AB = BC.
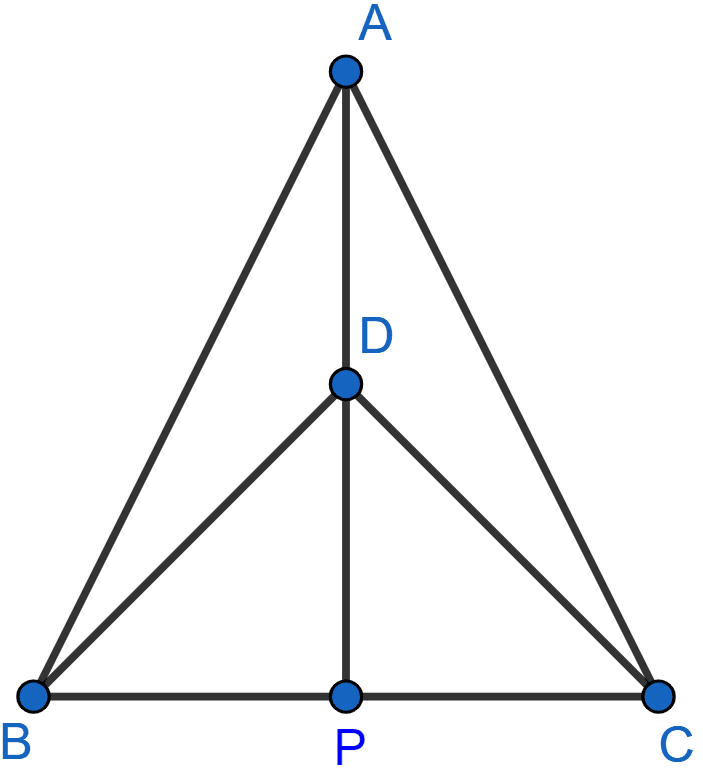
In the adjoining figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.