Mathematics
Answer
From figure,
∠ADC = ∠CAD (As angles opposite to equal sides of triangle are equal) ……(i)
From figure,
∠BAD = ∠BAC + ∠CAD = ∠BAC + ∠ADC = ∠BAC + ∠ADB …….(ii)
From △ABC,
∠BAC = ∠ACB (As angles opposite to equal sides of triangle are equal) ……(iii)
∠ACB = 180 - (∠ACD) = 180 - [180 - (∠CAD + ∠ADC)] = ∠CAD + ∠ADC ……..(iv)
From figure,
∠ADC = ∠ADB
∴ ∠CAD = ∠ADB
From (iv)
∠ACB = ∠CAD + ∠ADC = ∠ADB + ∠ADB = 2∠ADB.
From (iii) we get,
∠BAC = ∠ACB = 2∠ADB.
Substituting value of ∠BAC in (ii) we get,
∠BAD = ∠BAC + ∠ADB = 2∠ADB + ∠ADB = 3∠ADB.
Hence, ∠BAD : ∠ADB = 3∠ADB : ∠ADB = 3 : 1.
Hence, proved that ∠BAD : ∠ADB = 3 : 1.
Related Questions
In the figure (1) given below, ABC is an equilateral triangle. Base BC is produced to E, such that BC = CE. Calculate ∠ACE and ∠AEC.

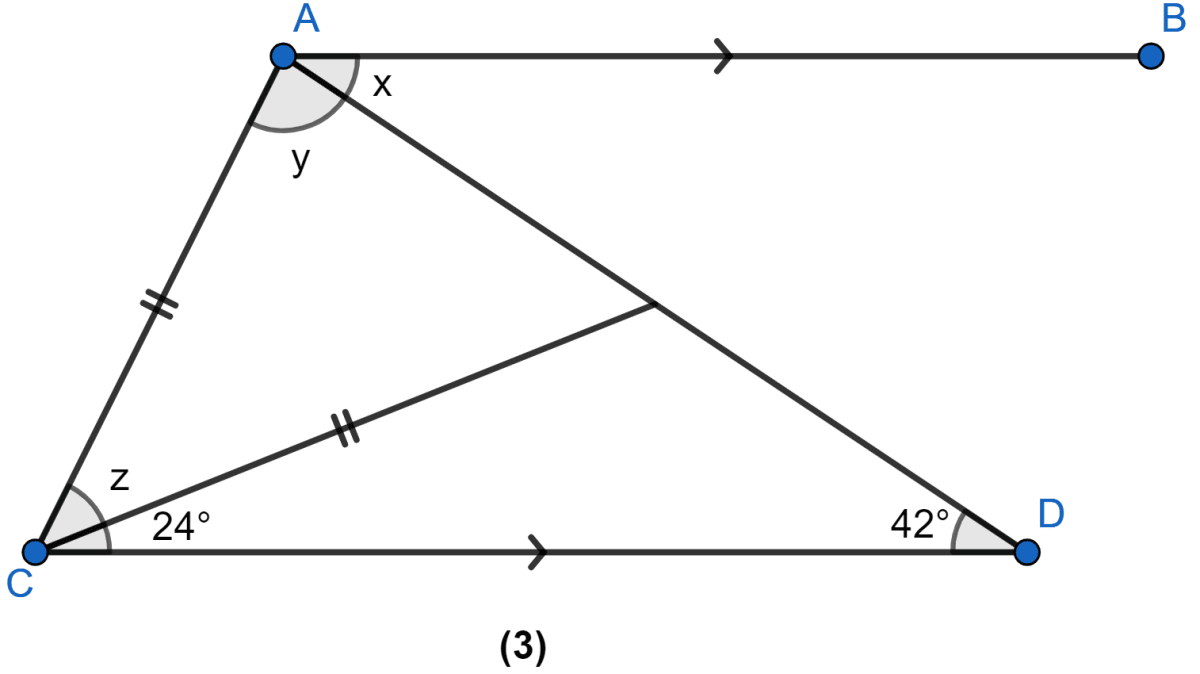
In the figure (3) given below, AB || CD. Find the values of x, y and z.
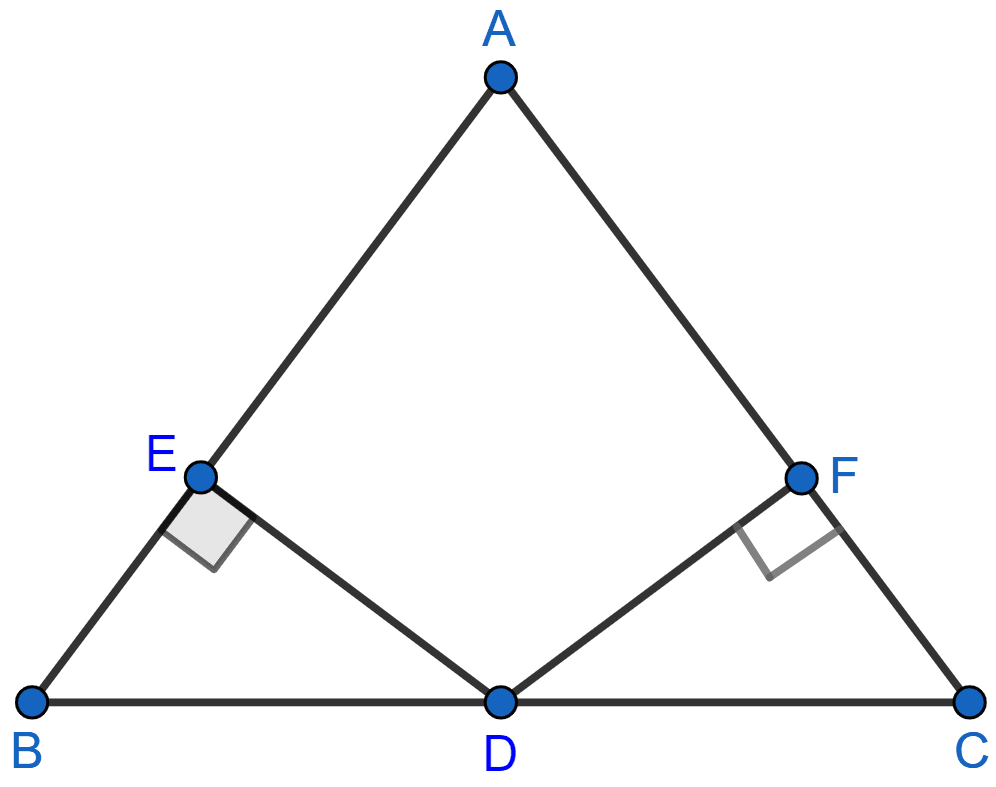
In the adjoining figure, D is the midpoint of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.