Mathematics
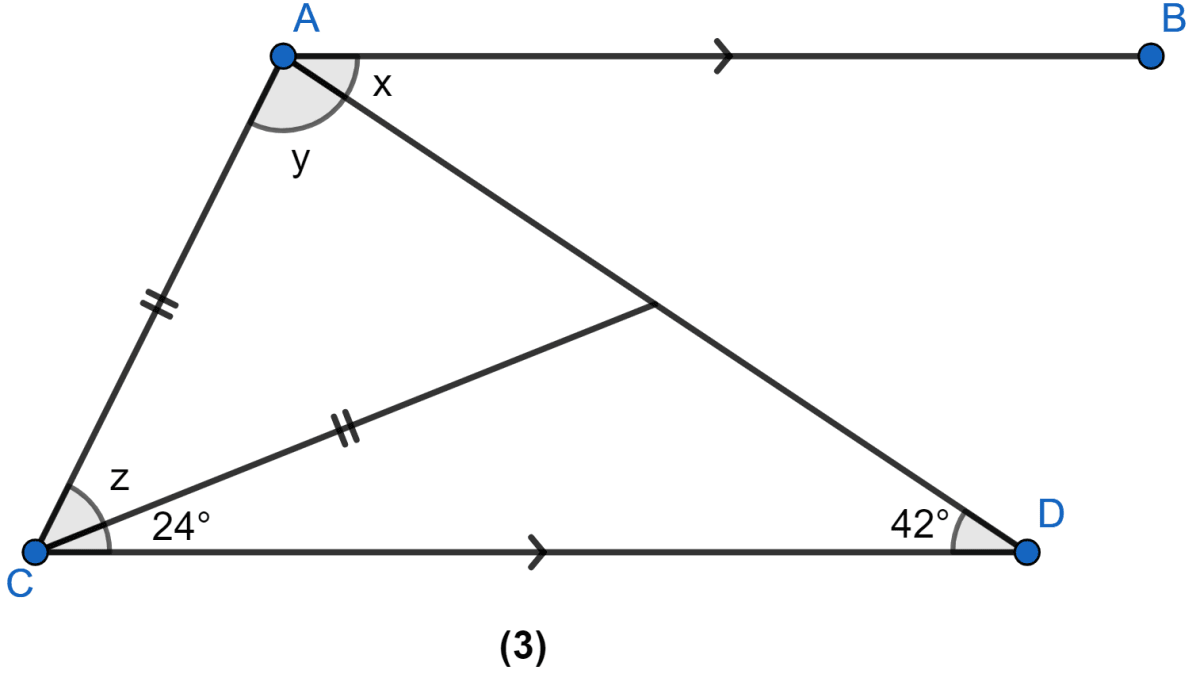
In the figure (3) given below, AB || CD. Find the values of x, y and z.
Triangles
40 Likes
Answer
From figure,
∠BAD = ∠ADC (Alternate angles)
∴ x = 42°
In △CED,
⇒ 24° + ∠CED + 42° = 180°
⇒ ∠CED + 66° = 180°
⇒ ∠CED = 114°.
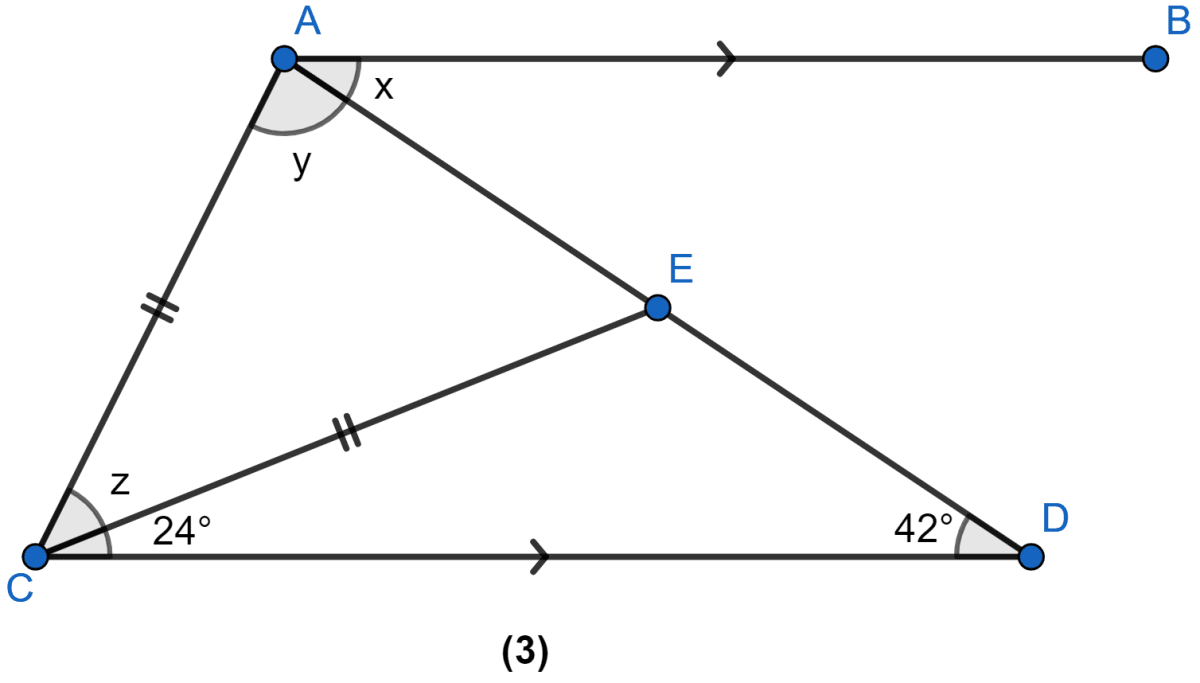
From figure,
⇒ ∠CEA + ∠CED = 180°
⇒ ∠CEA + 114° = 180°
⇒ ∠CEA = 66°.
In △CEA,
⇒ y = ∠CEA = 66° (As angles opposite to equal sides are equal)
In △CEA,
⇒ z + y + ∠CEA = 180°
⇒ z + 66° + 66° = 180°
⇒ z + 132° = 180°
⇒ z = 48°.
Hence, x = 42°, y = 66° and z = 48°.
Answered By
27 Likes
Related Questions
In the figure (1) given below, ABC is an equilateral triangle. Base BC is produced to E, such that BC = CE. Calculate ∠ACE and ∠AEC.

In the figure (2) given below, prove that ∠BAD : ∠ADB = 3 : 1.

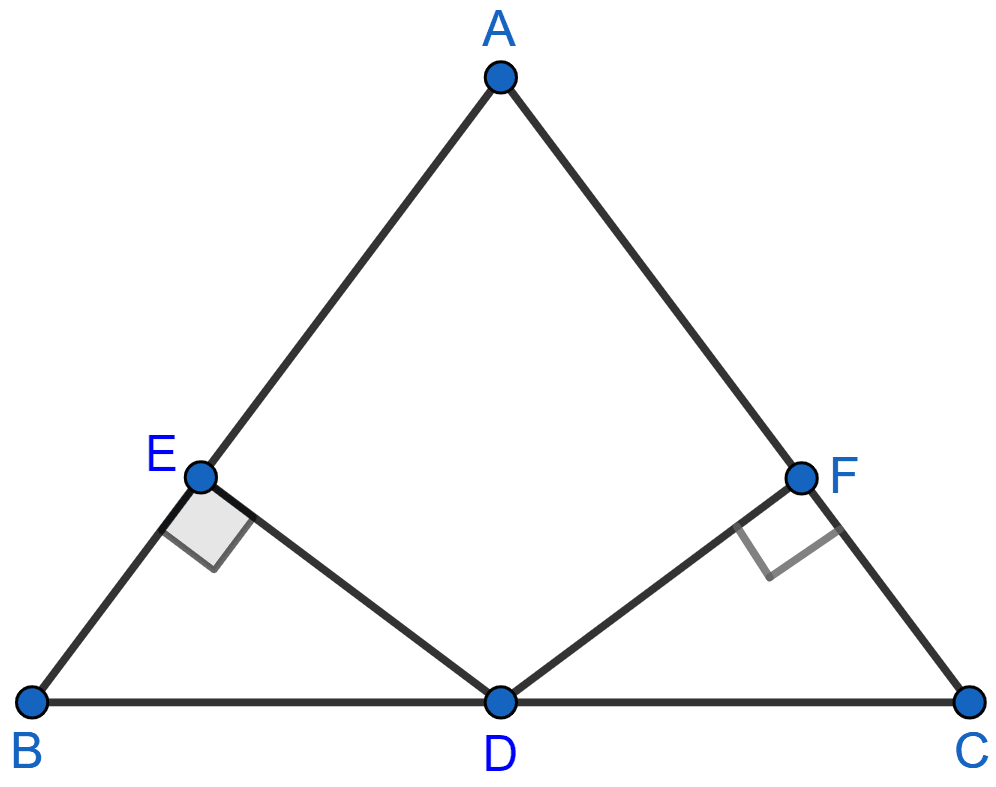
In the adjoining figure, D is the midpoint of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.
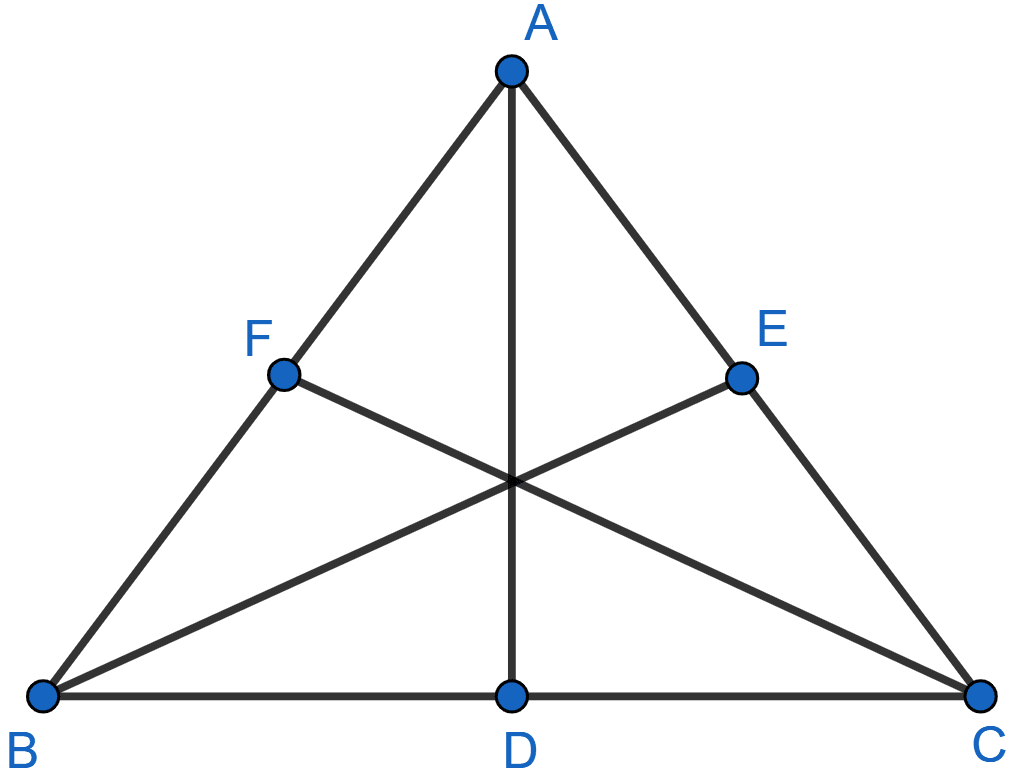
In the adjoining figure, AD, BE and CF are altitudes of △ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.