Mathematics
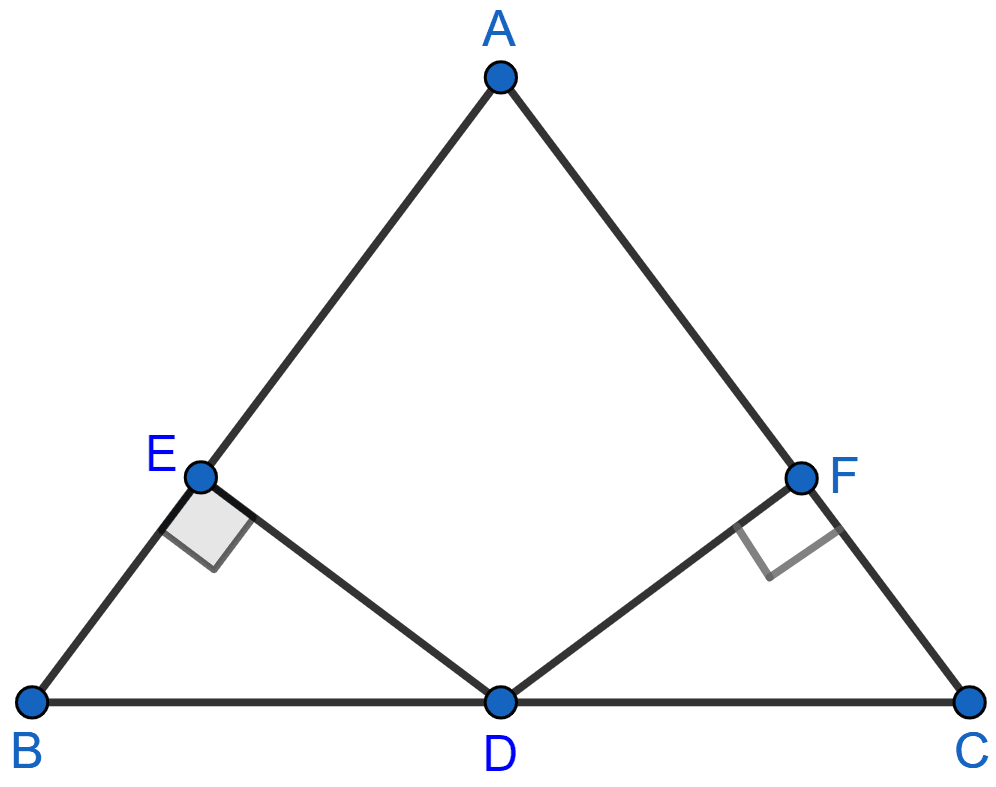
In the adjoining figure, D is the midpoint of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.
Triangles
65 Likes
Answer
In △BED and △CFD,
∠BED = ∠CFD (Both are equal to 90°)
DE = DF (Given)
BD = DC (As D is the mid-point of BC.)
∴ △BED ≅ △CFD by RHS axiom.
We know that corresponding parts of congruent triangles are equal,
∴ ∠B = ∠C ⇒ AC = AB.
Hence, proved that ABC is an isosceles triangle.
Answered By
46 Likes
Related Questions
In the figure (2) given below, prove that ∠BAD : ∠ADB = 3 : 1.

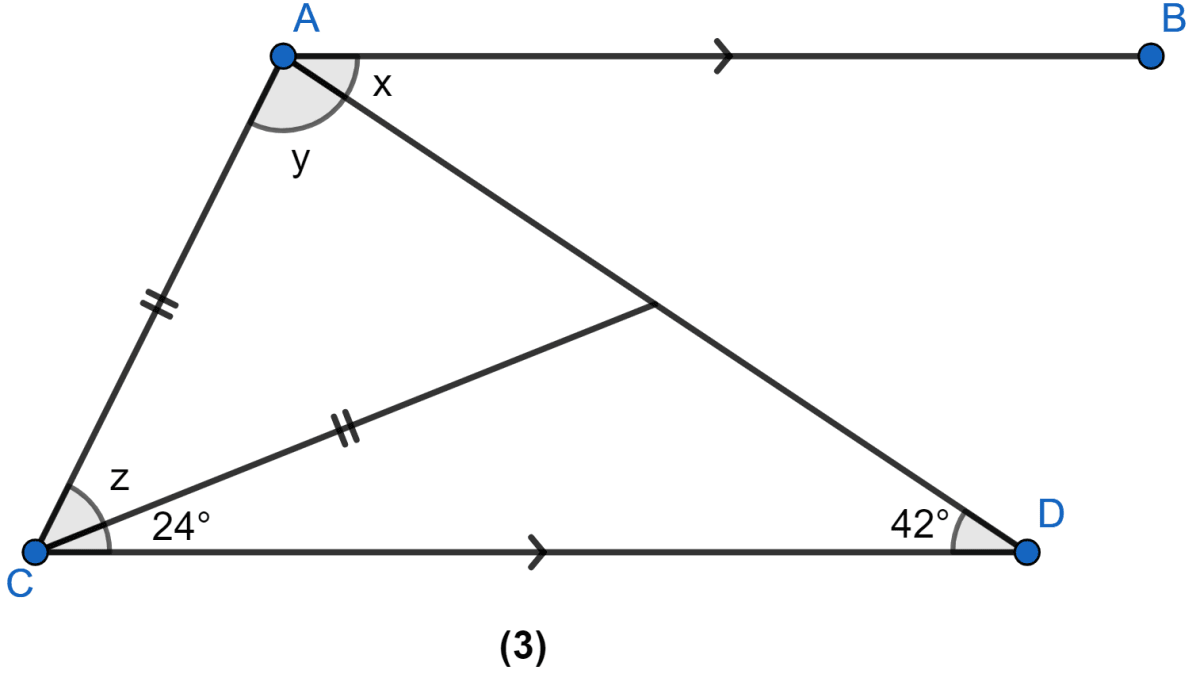
In the figure (3) given below, AB || CD. Find the values of x, y and z.
In the adjoining figure, AD, BE and CF are altitudes of △ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.
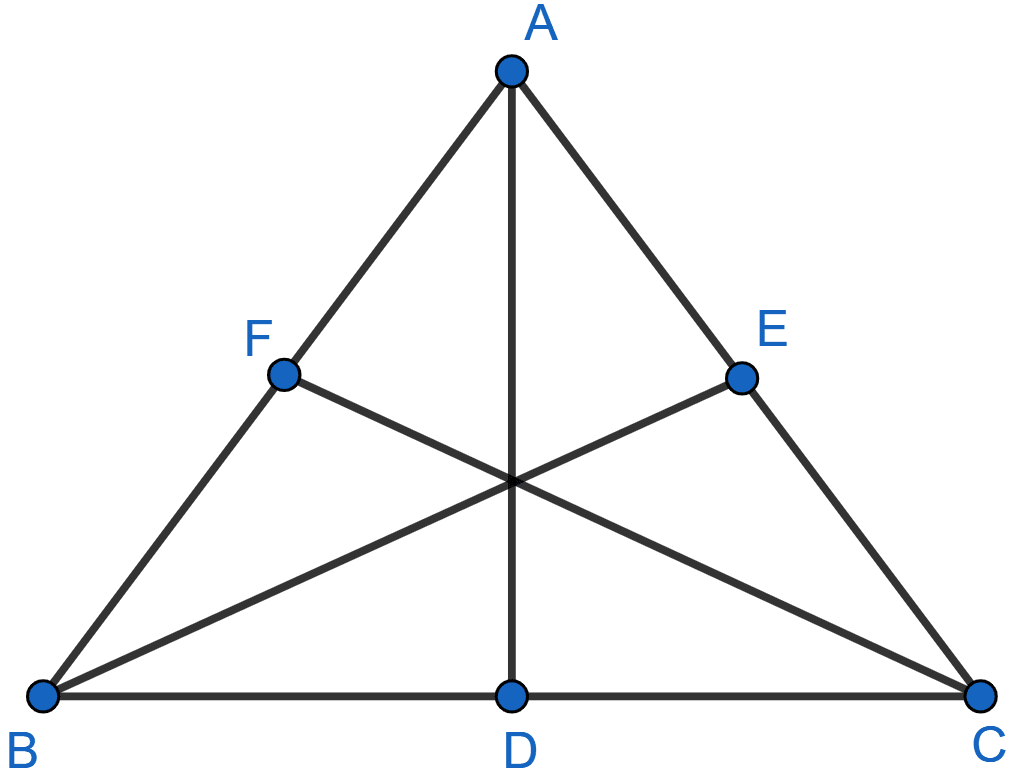
In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) △DBC ≅ △ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.