Mathematics
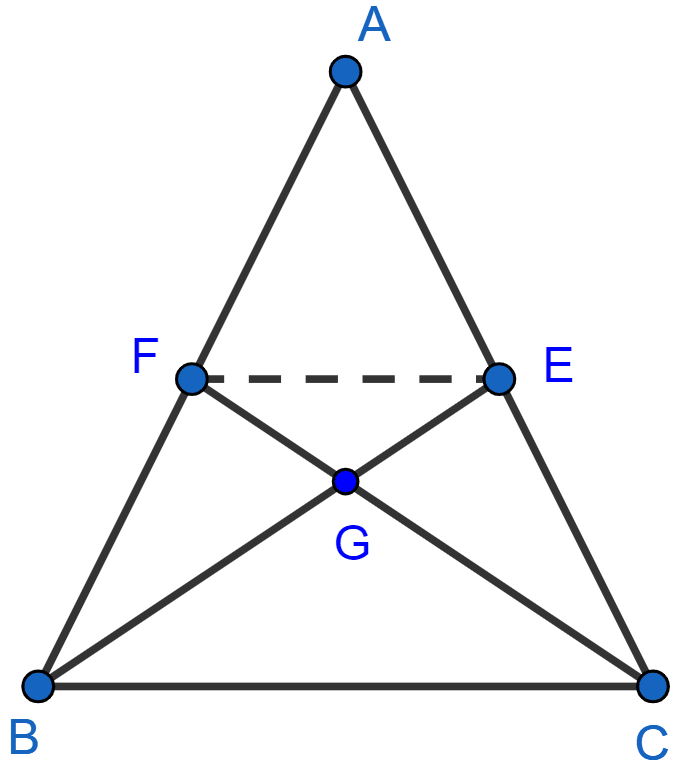
In the figure (2) given below, medians BE and CF of a △ABC meet at G. Prove that :
(i) △FGE ~ △CGB
(ii) BG = 2GE
Similarity
22 Likes
Answer
(i) Considering △FGE and △CGB,
∠FGE = ∠BGC (Vertically opposite angles are equal)
∠GFE = ∠GCB (Alternate angles are equal)
Hence by AA axiom △FGE ~ △CGB.
(ii) Considering △AFE and △ABC,
∠A = ∠A (Common angles)
∠AFE = ∠ABC (Corresponding angles are equal)
Hence by AA axiom △AFE ~ △ABC.
Given BE is the median of AC, so
AE = EC
AC = AE + EC = AE + AE = 2AE.
Since, △AFE ~ △ABC, so the ratio of their corresponding sides are equal,
Since, △FGE ~ △CGB, so the ratio of their corresponding sides are equal,
Hence, proved that BG = 2GE.
Answered By
14 Likes
Related Questions
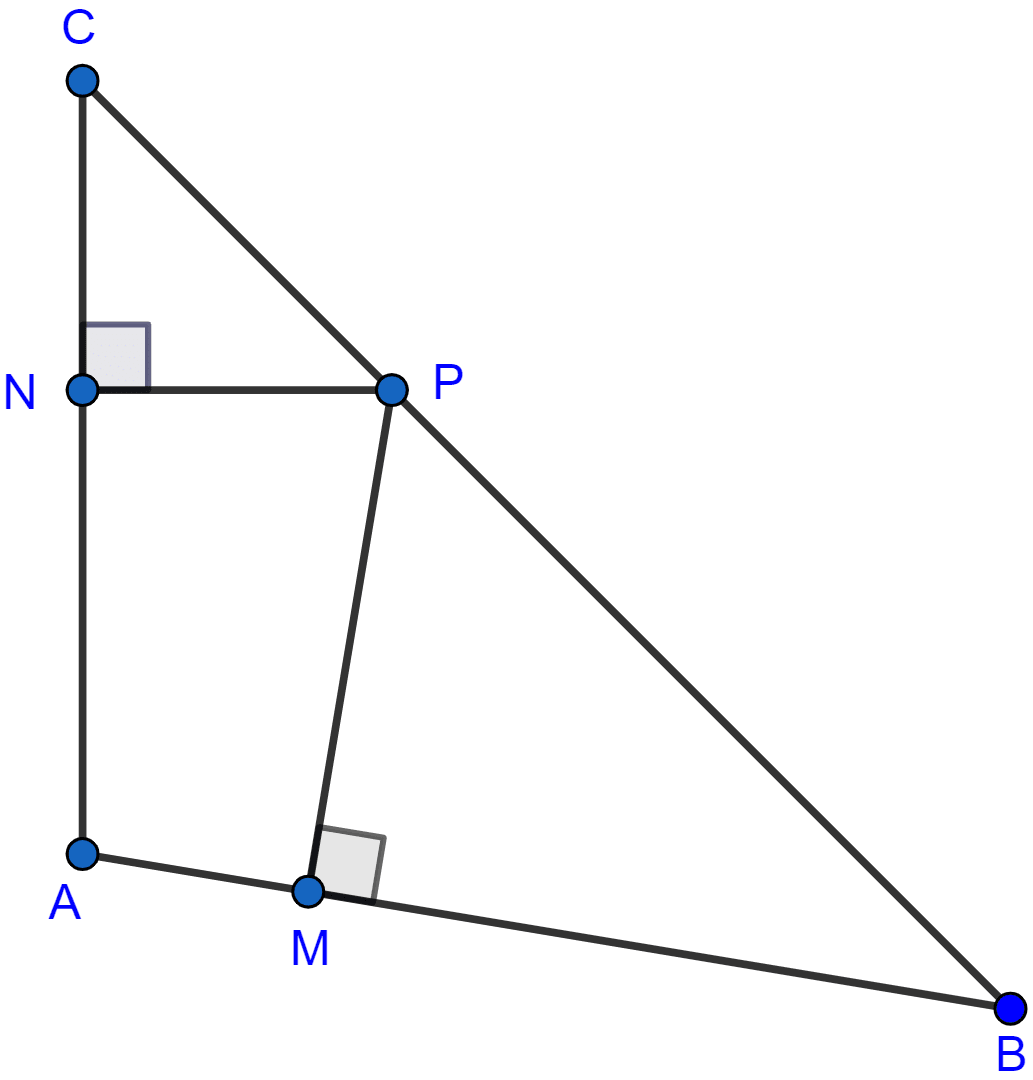
In the adjoining figure, AB = AC. If PM ⊥ AB and PN ⊥ AP, show that PM × PC = PN × PB.
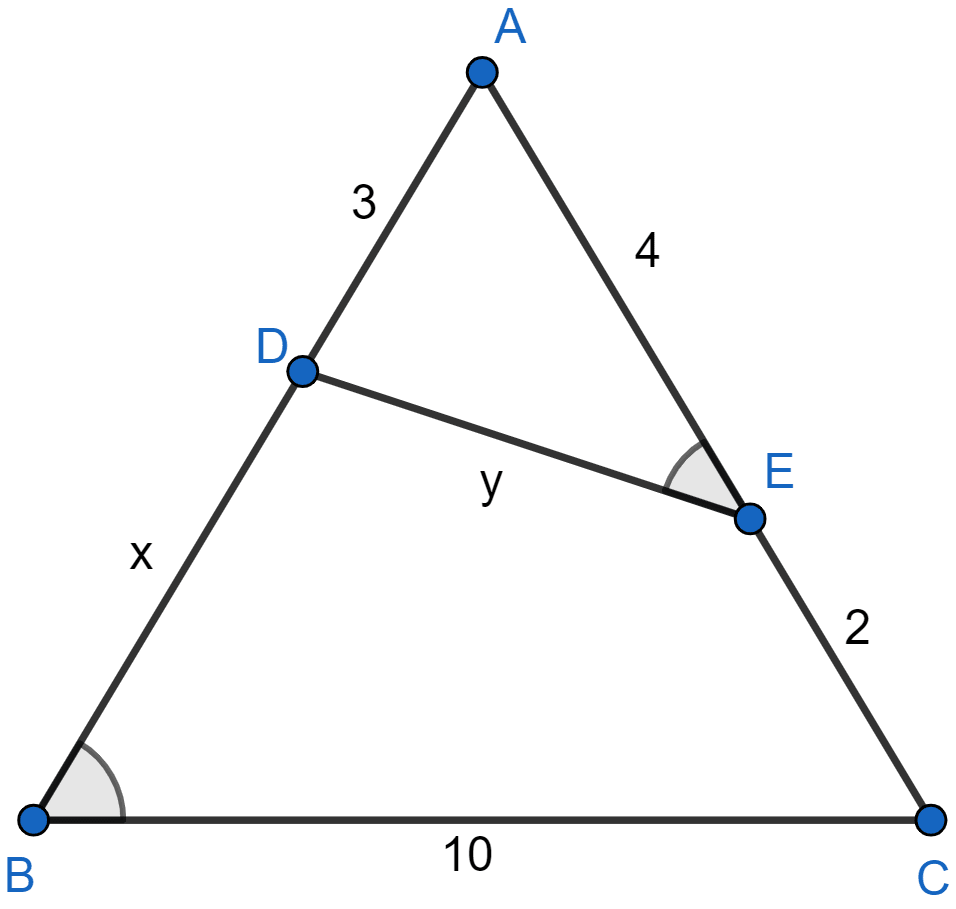
In the figure (1) given below, ∠AED = ∠ABC. Find the values of x and y.
In the given figure, P is a point on AB such that PB : AP = 3 : 4 and PQ || AC.
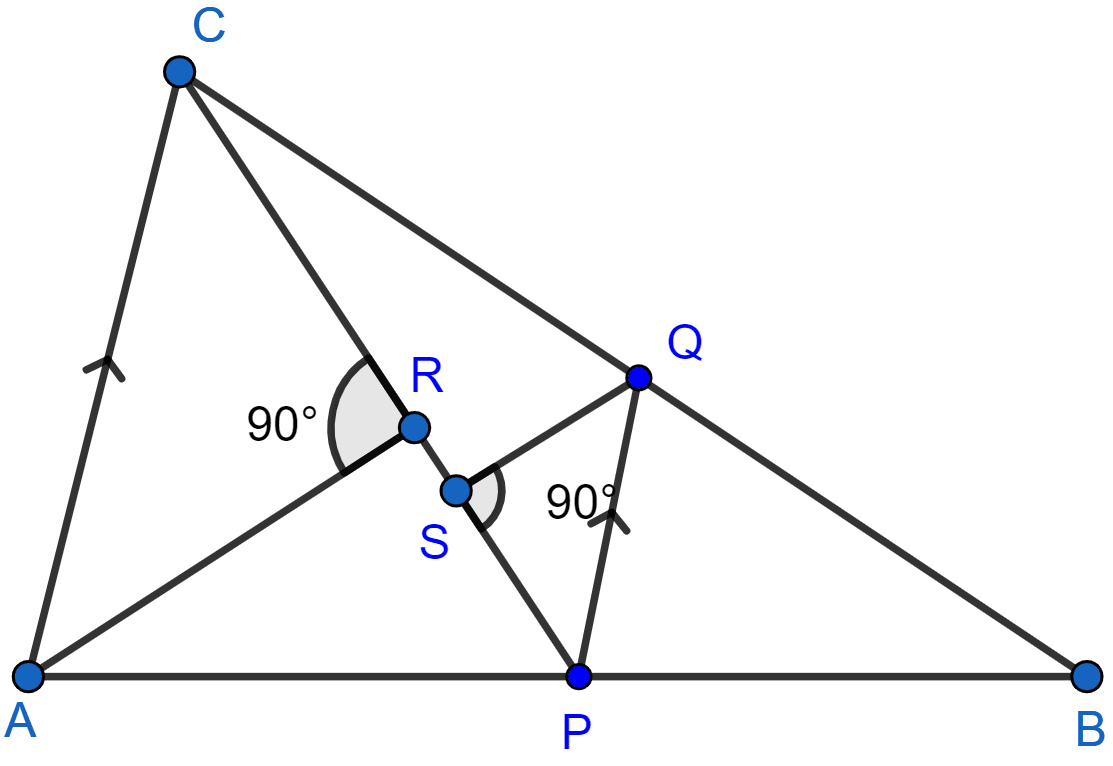
(i) Calculate PQ : AC.
(ii) If AR ⊥ CP, QS ⊥ CB and QS = 6 cm, calculate the length of AR.
In a △ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE.