Mathematics
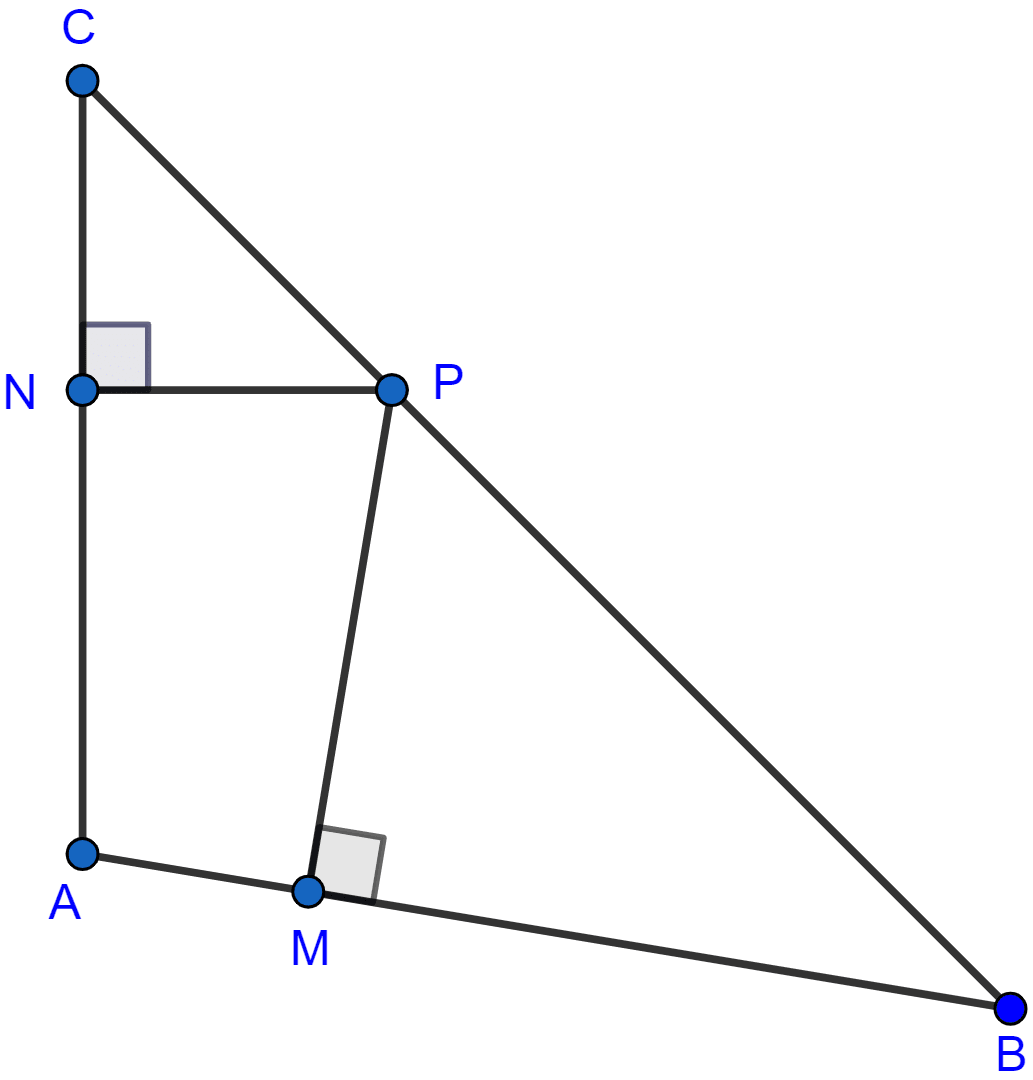
In the adjoining figure, AB = AC. If PM ⊥ AB and PN ⊥ AP, show that PM × PC = PN × PB.
Similarity
22 Likes
Answer
Considering △PNC and △PMB,
∠PNC = ∠PMB (Both are equal to 90°)
∠NCP = ∠PBM (As AB = AC)
Hence by AA axiom △PNC ~ △PMB.
Since, triangles are similar so ratio of their corresponding sides will be equal.
Hence, proved that PC × PM = PN × PB.
Answered By
16 Likes
Related Questions
Given Δ ABC ∼ Δ DEF.
Assertion (A): If area of Δ ABC = 64 cm2, area of Δ DEF = 49 cm2 and BC = 4 cm, then EF is 7 cm.
Reason (R): The ratio of area of two similar triangle is equal to the ratio of square of their corresponding sides.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
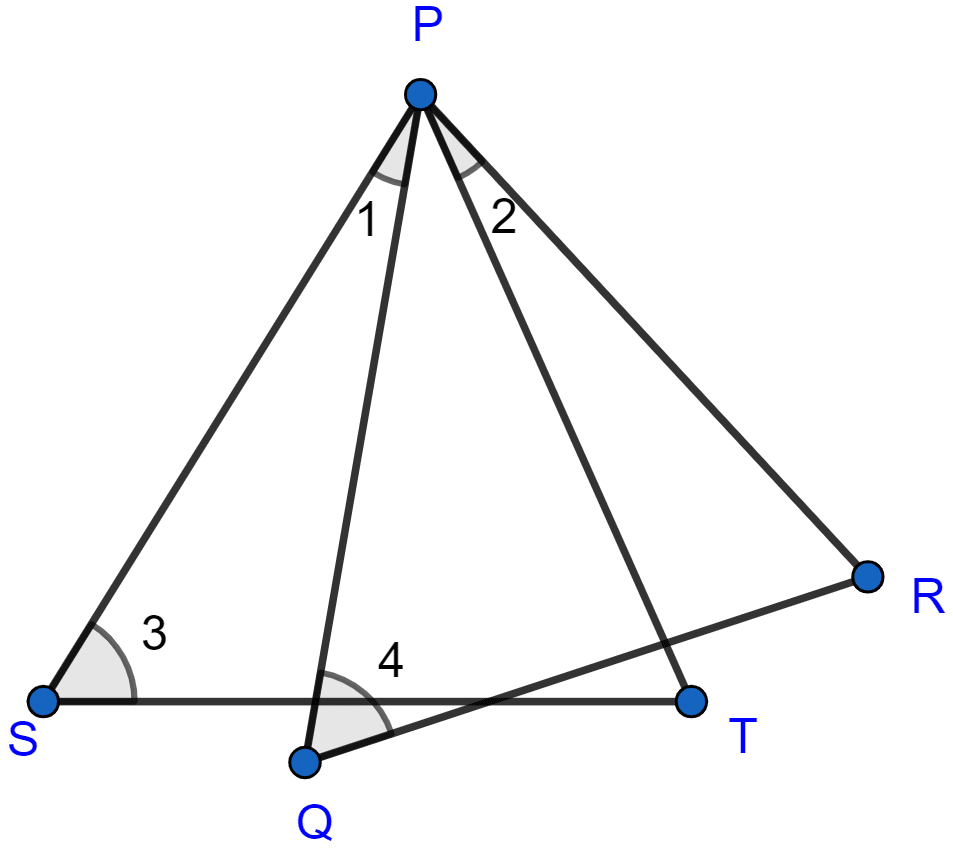
In the adjoining figure, ∠1 = ∠2 and ∠3 = ∠4. Show that PT × QR = PR × ST.
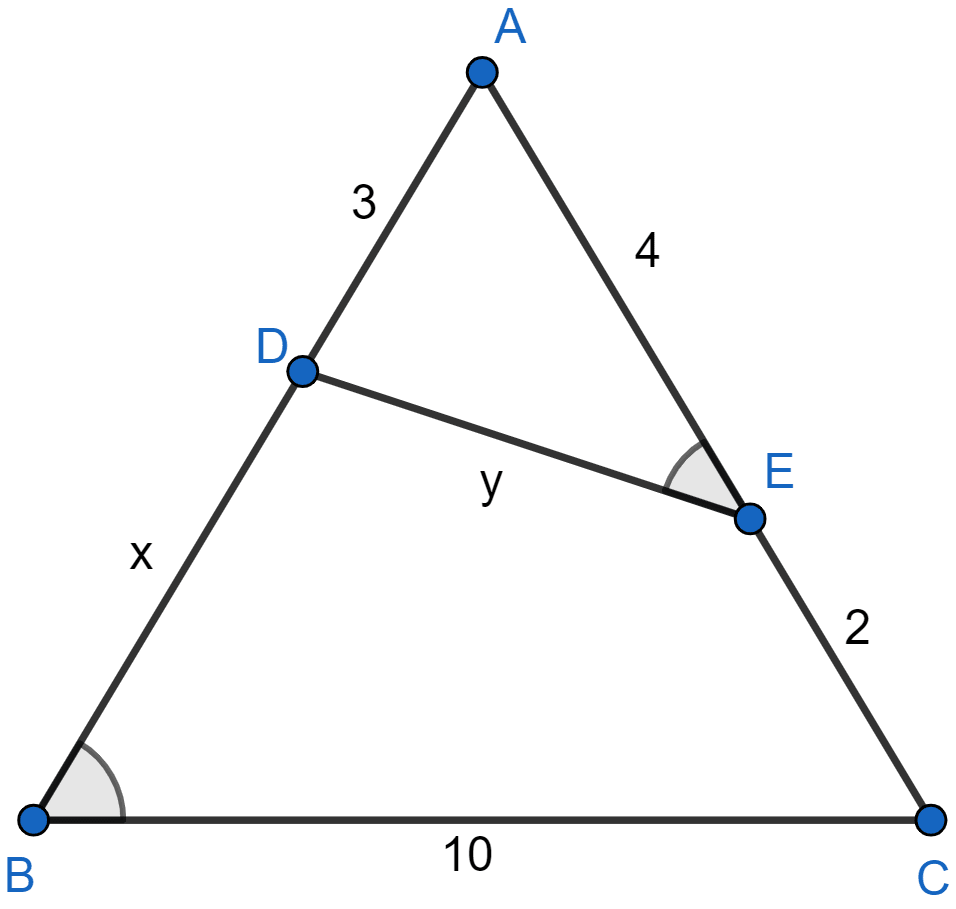
In the figure (1) given below, ∠AED = ∠ABC. Find the values of x and y.
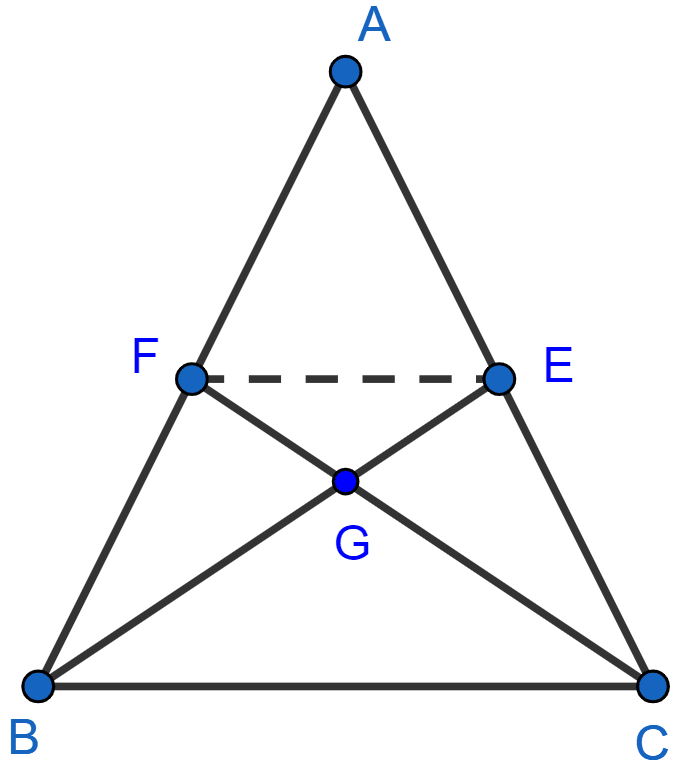
In the figure (2) given below, medians BE and CF of a △ABC meet at G. Prove that :
(i) △FGE ~ △CGB
(ii) BG = 2GE