Mathematics
In the figure (2) given below, BC = CD. Find ∠ACB.

Triangles
68 Likes
Answer
From figure,
∠DAC = 180° - 138° = 42°.
∠BDC = 180° - ∠ADC = 180° - 116° = 64°.
In △BCD,
∠CBD = ∠BDC = 64°.
∠DCB = 180° - (∠CBD + ∠BDC) = 180° - (64° + 64°)
= 180° - 128° = 52°.
In △ADC,
∠DCA = 180° - (∠CAD + ∠ADC) = 180° - (42° + 116°)
= 180° - 158° = 22°.
From figure,
∠ACB = ∠DCB + ∠DCA = 52° + 22° = 74°.
Hence, ∠ACB = 74°.
Answered By
29 Likes
Related Questions
In the following figure, find the value of x:

In the figure (1) given below, AB = AD, BC = DC. Find ∠ABC.

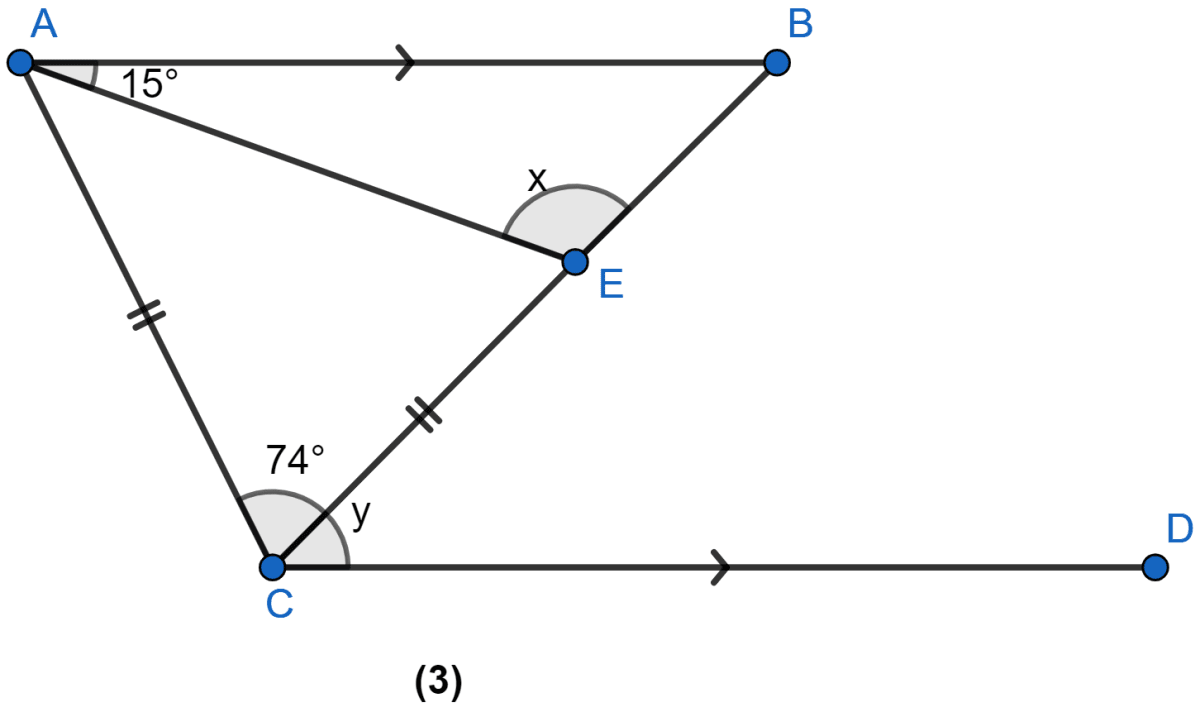
In the figure (3) given below, AB || CD and CA = CE. If ∠ACE = 74° and ∠BAE = 15°, find the values of x and y.
In △ABC, AB = AC, ∠A = (5x + 20)° and each of the base angle is th of ∠A. Find the measure of ∠A.