Mathematics
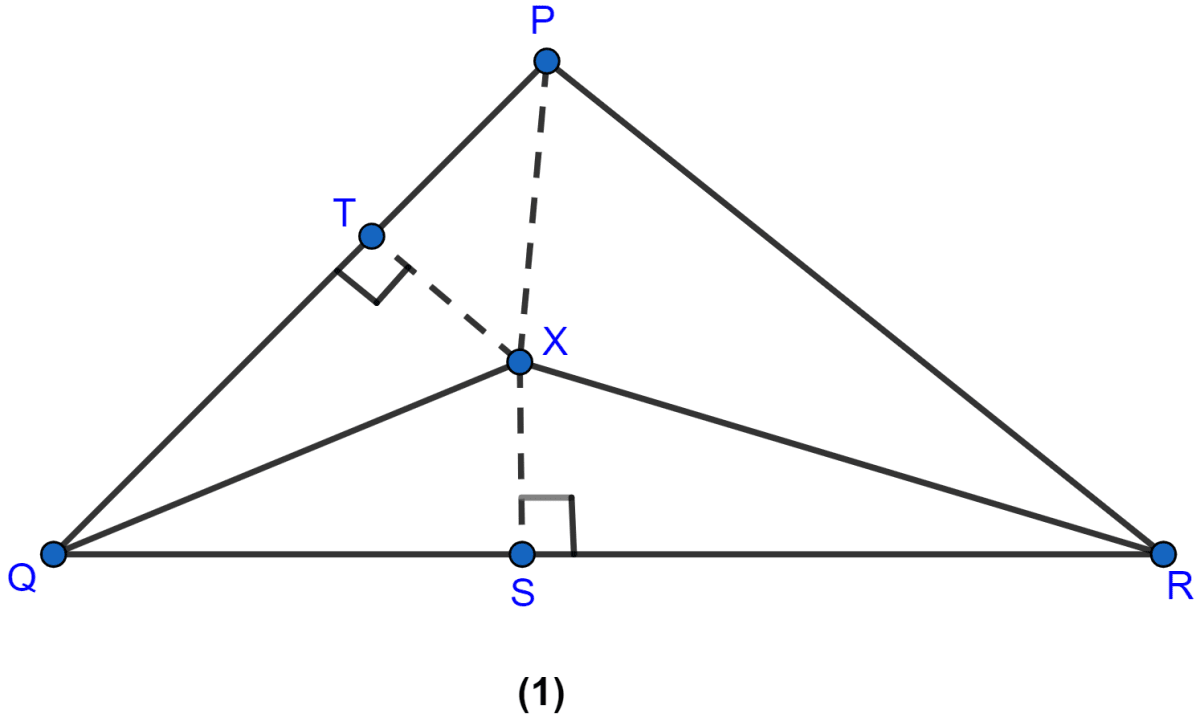
In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of △PQR. If XS ⊥ QR and XT ⊥ PQ, prove that
(i) △XTQ ≅ △XSQ
(ii) PX bisects the angle P.
Answer
(i) Given, QX is the bisector of ∠PQR
∴ ∠PQX = ∠XQS
From figure,
∠XTQ = ∠XSQ (Both are equal to 90°)
XQ = XQ
Hence, △XTQ ≅ △XSQ by ASA axiom.
Hence, proved that △XTQ ≅ △XSQ.
(ii) Draw a perpendicular from X on PR i.e. XU.
In △XSR and △XUR,
∠XSR = ∠XUR (Both are equal to 90°)
∠XRS = ∠XRU (As XR is bisector)
XR = XR (Common)
Hence, △XSR ≅ △XUR by AAS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ XU = XS ……..(i)
As, △XTQ ≅ △XSQ
∴ XS = XT …….(ii)
In △XUP and △XTP,
From (i) and (ii) we get,
XU = XT
XP = XP (Common)
∠XTP = ∠XUP (Both are equal to 90°)
Hence, △XUP ≅ △XTP by SAS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ ∠XPU = ∠XPT
Hence, proved that PX is bisector of ∠P.
Related Questions
In the adjoining figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that △ABC ≅ △DEF.

ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In the figure (2) given below, AB || DC and ∠C = ∠D. Prove that
(i) AD = BC
(ii) AC = BD.

In the figure (3) given below, BA || DF and CA || EG and BD = EC. Prove that
(i) BG = DF
(ii) EG = CF.
