Mathematics
In the figure (3) given below, BA || DF and CA || EG and BD = EC. Prove that
(i) BG = DF
(ii) EG = CF.

Triangles
48 Likes
Answer
Given,
BD = EC
BD + DE = DE + EC
BE = DC.
Considering △BGE and △DFC,
∠GBE = ∠FDC (Corresponding angles)
∠GEB = ∠FCD (Corresponding angles)
BE = DC (Proved).
∴ △BGE ≅ △DFC by ASA axiom..
We know that corresponding parts of congruent triangles are equal.
∴ BG = DF.
Hence, proved that BG = DF.
(ii) We know,
△BGE ≅ △DFC.
We know that corresponding parts of congruent triangles are equal.
∴ EG = CF.
Hence, proved that EG = CF.
Answered By
27 Likes
Related Questions
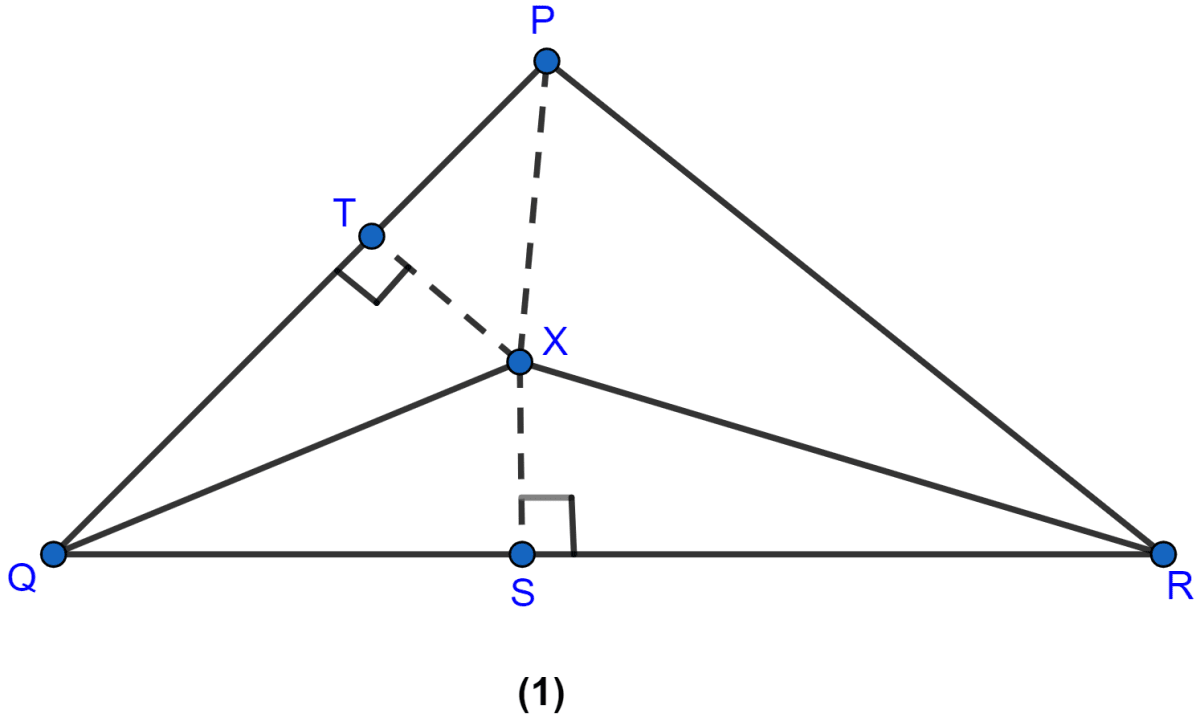
In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of △PQR. If XS ⊥ QR and XT ⊥ PQ, prove that
(i) △XTQ ≅ △XSQ
(ii) PX bisects the angle P.
In the figure (2) given below, AB || DC and ∠C = ∠D. Prove that
(i) AD = BC
(ii) AC = BD.

In the following figure, find the values of x and y.

In the following figure, find the values of x and y.
