Mathematics
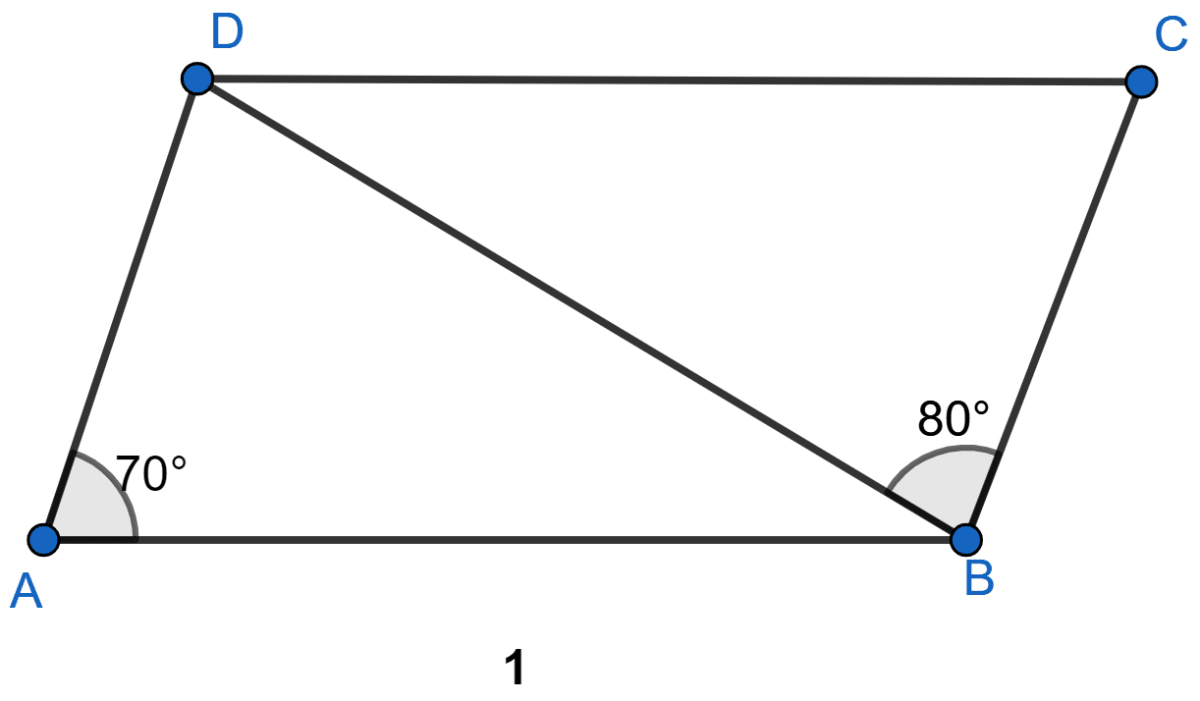
In the figure (1) given below, ABCD is a parallelogram in which ∠DAB = 70°, ∠DBC = 80°. Calculate angles CDB and ADB.
Rectilinear Figures
59 Likes
Answer
As AD || BC, sum of co-int ∠s = 180°.
∠A + ∠B = 180°
∠B = 180° - ∠A = 180° - 70° = 110°.
From figure,
⇒ ∠B = ∠DBA + ∠DBC
⇒ 110° = ∠DBA + 80°
⇒ ∠DBA = 110° - 80° = 30°.
Sum of angles of a triangle = 180°
In △DAB,
⇒ ∠DAB + ∠DBA + ∠ADB = 180°
⇒ 70° + 30° + ∠ADB = 180°
⇒ ∠ADB = 180° - 100° = 80°.
Since, opposite angles of a parallelogram are equal,
∴ ∠C = ∠A = 70°.
In △DBC,
⇒ ∠DBC + ∠BCD + ∠CDB = 180°
⇒ 80° + 70° + ∠CDB = 180°
⇒ ∠CDB = 180° - 150° = 30°.
Hence, ∠ADB = 80° and ∠CDB = 30°.
Answered By
32 Likes
Related Questions
If the angles of a quadrilateral, taken in order, are in the ratio 1 : 2 : 3 : 4, prove that it is a trapezium.
If an angle of a parallelogram is two-thirds of its adjacent angle, find the angles of the parallelogram.
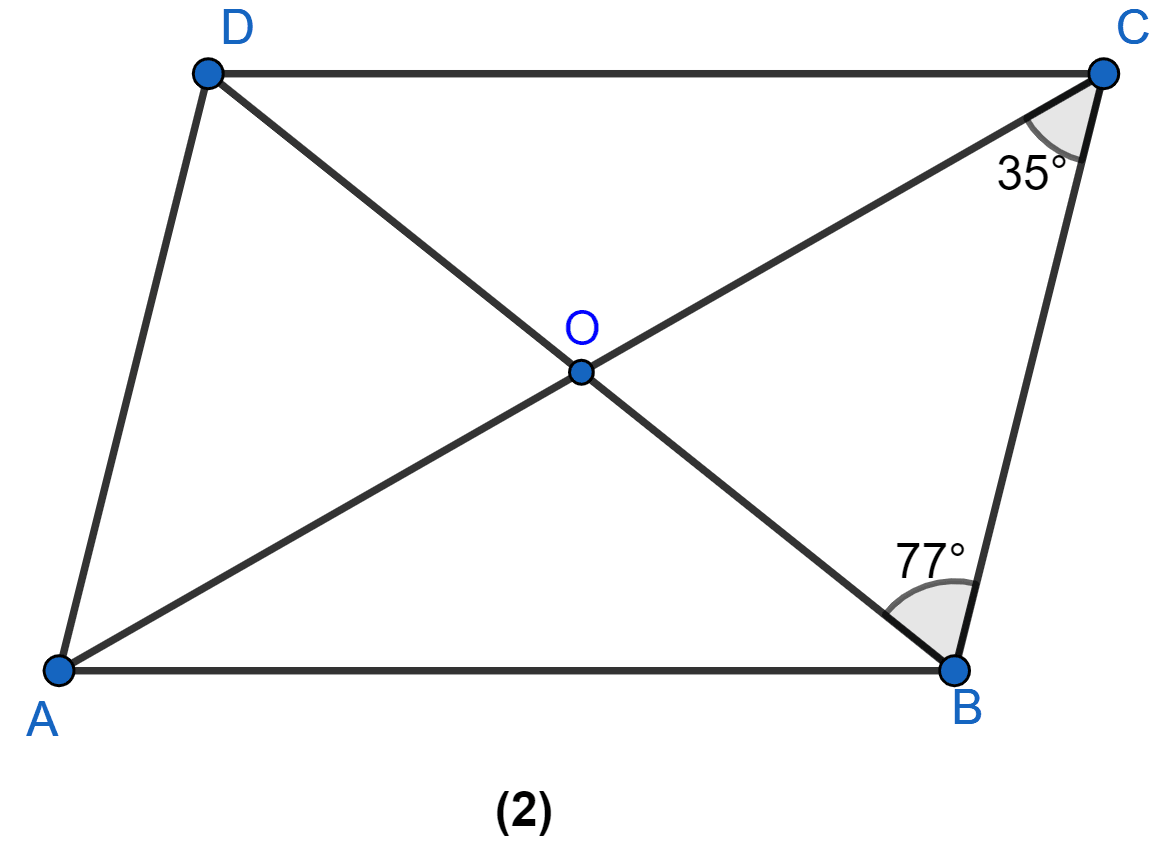
In figure (2) given below, ABCD is a parallelogram. Find the angles of △AOD.
In figure (3) given below, ABCD is a rhombus. Find the value of x.
