Mathematics
If the angles of a quadrilateral, taken in order, are in the ratio 1 : 2 : 3 : 4, prove that it is a trapezium.
Rectilinear Figures
58 Likes
Answer
Let a trapezium be ABCD.
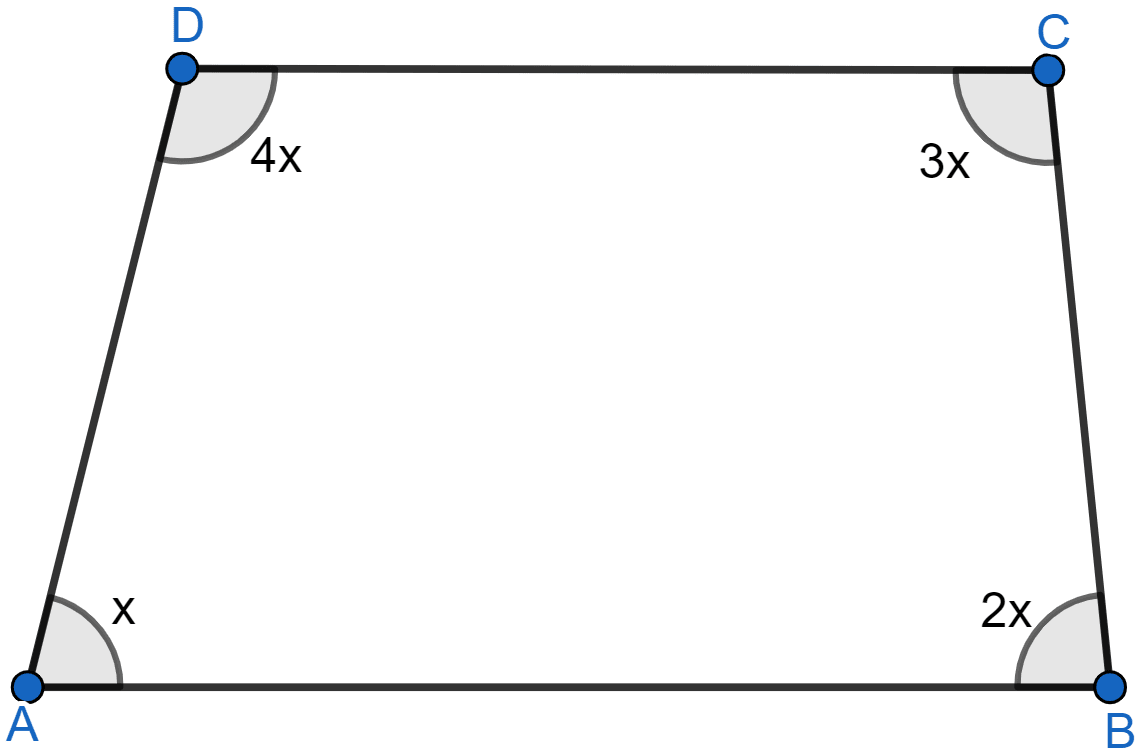
Let angles be x, 2x, 3x and 4x taken in order.
Sum of angles of quadrilateral = 360°.
∴ x + 2x + 3x + 4x = 360°
⇒ 10x = 360°
⇒ x =
⇒ x = 36°.
⇒ ∠A = x = 36°,
⇒ ∠B = 2x = 2(36°) = 72°
⇒ ∠C = 3x = 3(36°) = 108°
⇒ ∠D = 2x = 4(36°) = 144°.
From figure,
∠A and ∠D are co-interior angles and their sum = 180° (36° + 144°).
Sum of co-interior angles = 180°, which means AB and CD are parallel.
Also,
Opposite angles sum i.e.
∠A + ∠C = 36° + 108° = 144°,
∠B + ∠D = 72° + 144° = 216°.
Since, the sum of opposite angles ≠ 180° (Property of trapezium).
Hence, proved that ABCD is a trapezium.
Answered By
40 Likes
Related Questions
If two angles of a quadrilateral are 40° and 110° and the other two are in the ratio 3 : 4, find these angles.
If an angle of a parallelogram is two-thirds of its adjacent angle, find the angles of the parallelogram.
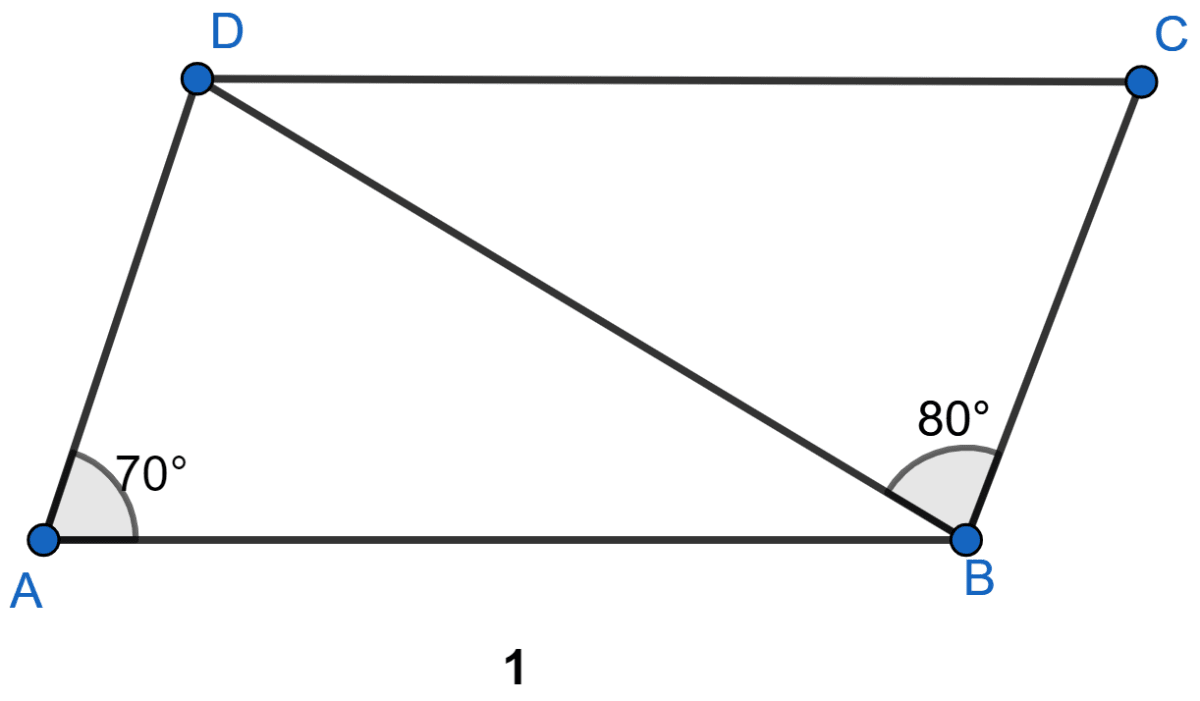
In the figure (1) given below, ABCD is a parallelogram in which ∠DAB = 70°, ∠DBC = 80°. Calculate angles CDB and ADB.
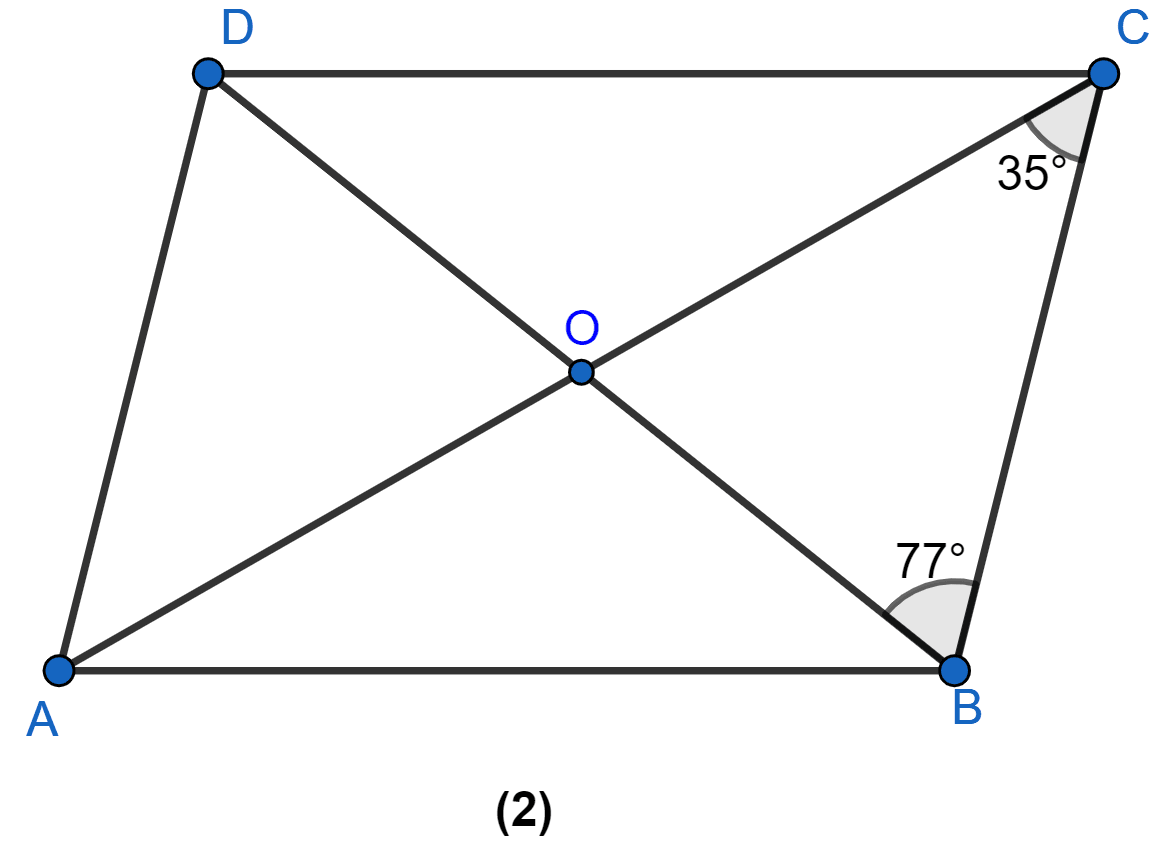
In figure (2) given below, ABCD is a parallelogram. Find the angles of △AOD.