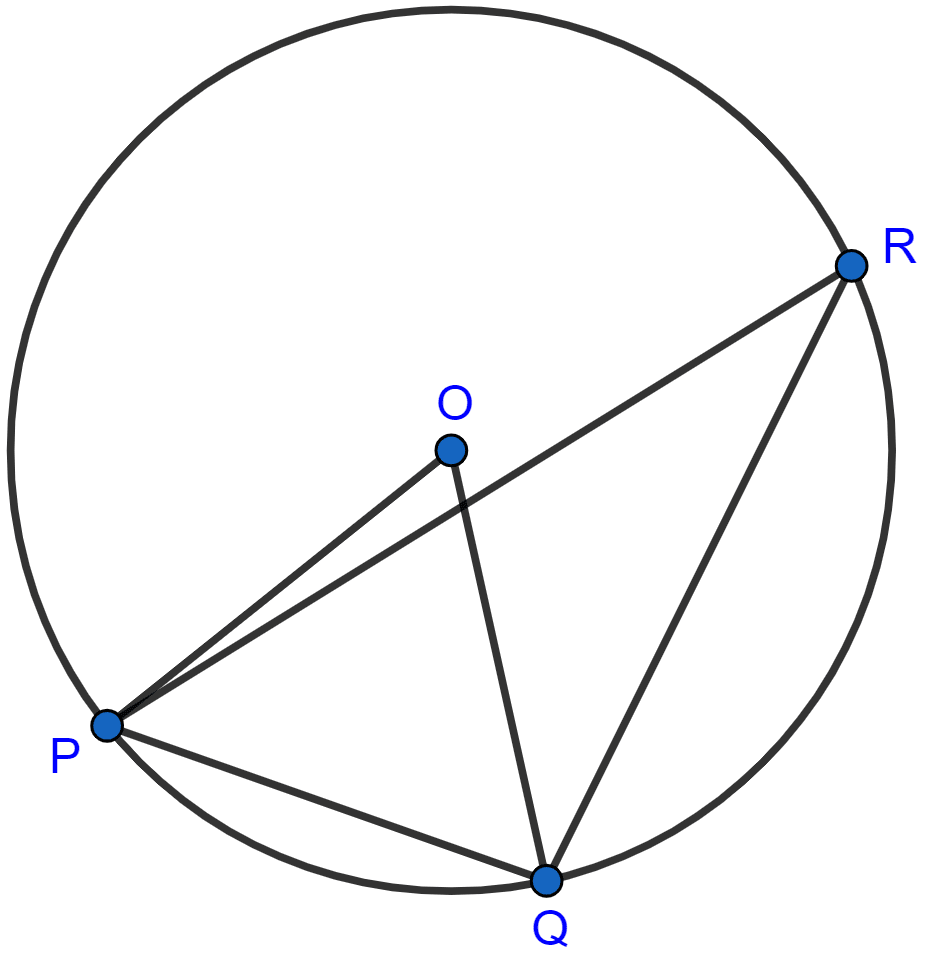
In the adjoining figure, O is the centre of the circle. If the length of the chord PQ is equal to the radius of the circle, then ∠PRQ is

1. 60°

2. 45°

3. 30°

4. 15°

From figure,

In △OPQ,

OP = OQ = PQ = (Radius of the circle.)

Hence, △OPQ is an equilateral triangle.

∴ ∠POQ = 60° (∵ all angles of an equilateral triangle = 60°.)

Arc PQ subtends ∠POQ at centre and ∠PRQ at remaining part of circle.

∠POQ = 2∠PRQ (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)

60° = 2∠PRQ

∠PRQ = $\dfrac{60°}{2}$ = 30°.

Hence, Option 3 is the correct option.