Mathematics
From a point which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
60 cm2
65 cm2
30 cm2
32.5 cm2
Circles
3 Likes
Answer
Given, the point P is 13 cm from O, the centre of the circle as shown in the figure below:
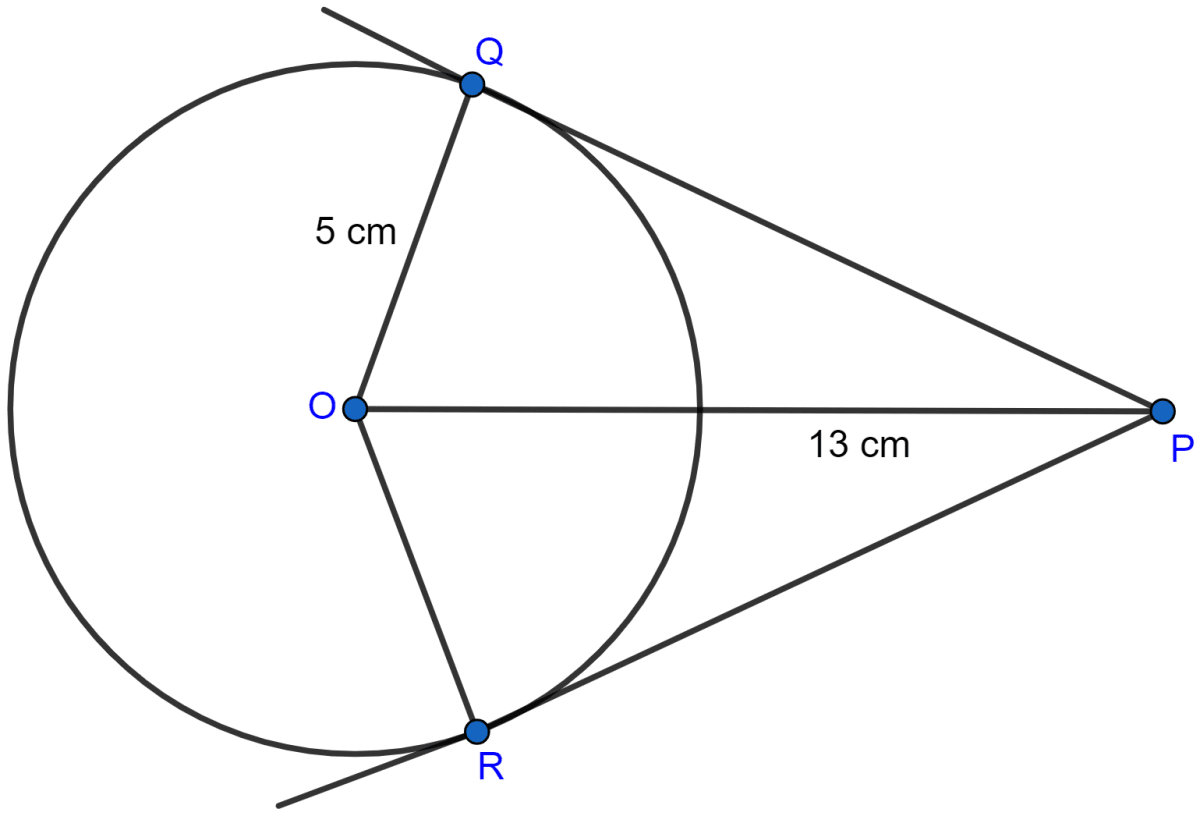
Radius of the circle (OQ) = 5 cm
PQ and PR are tangents from P to the circle.
PQ ⊥ OQ (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ OQP = 90°.
So, in △OQP,
Area of △OPQ = = cm2.
Similarly,
PR ⊥ OR (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ORP = 90°.
So, in △ORP,
Area of △POR = = cm2.
Area of quadrilateral PQOR = Area of △POR + Area of △OPQ = 30 + 30 = 60 cm2.
Hence, Option 1 is the correct option.
Answered By
1 Like
Related Questions
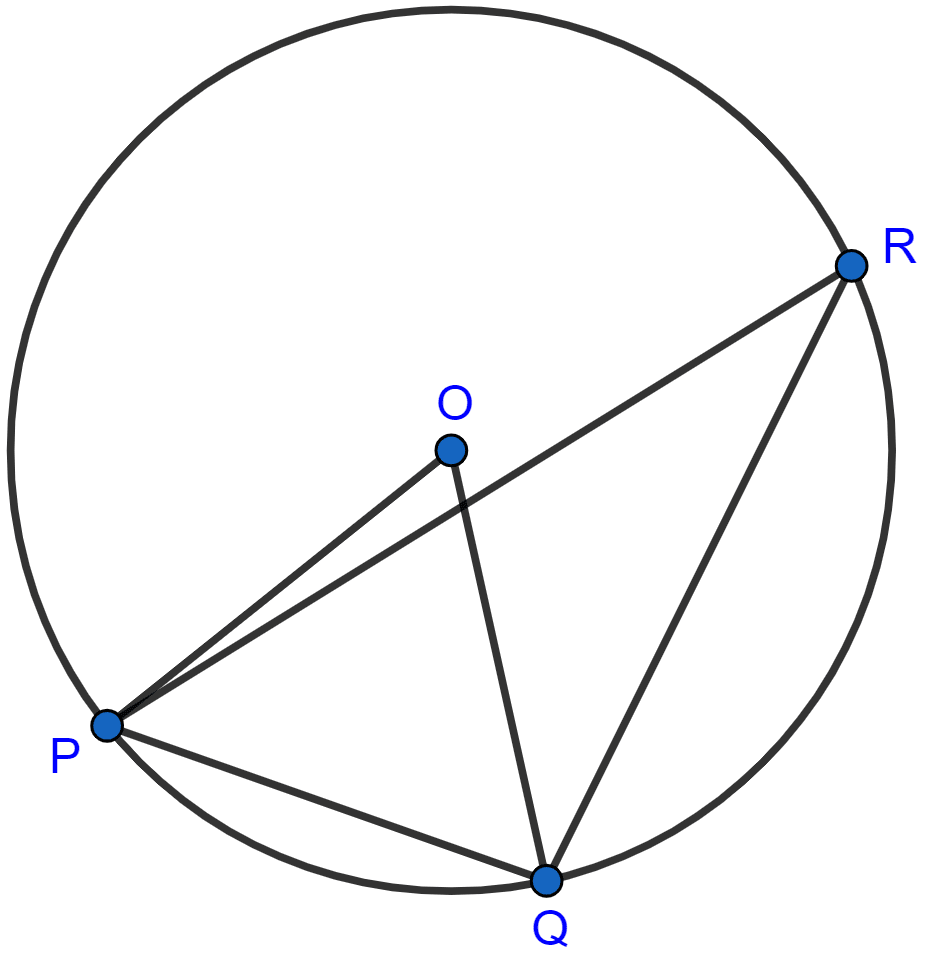
In the adjoining figure, O is the centre of the circle. If the length of the chord PQ is equal to the radius of the circle, then ∠PRQ is
60°
45°
30°
15°
In the adjoining figure, if O is the centre of the circle then the value of x is
18°
20°
24°
36°

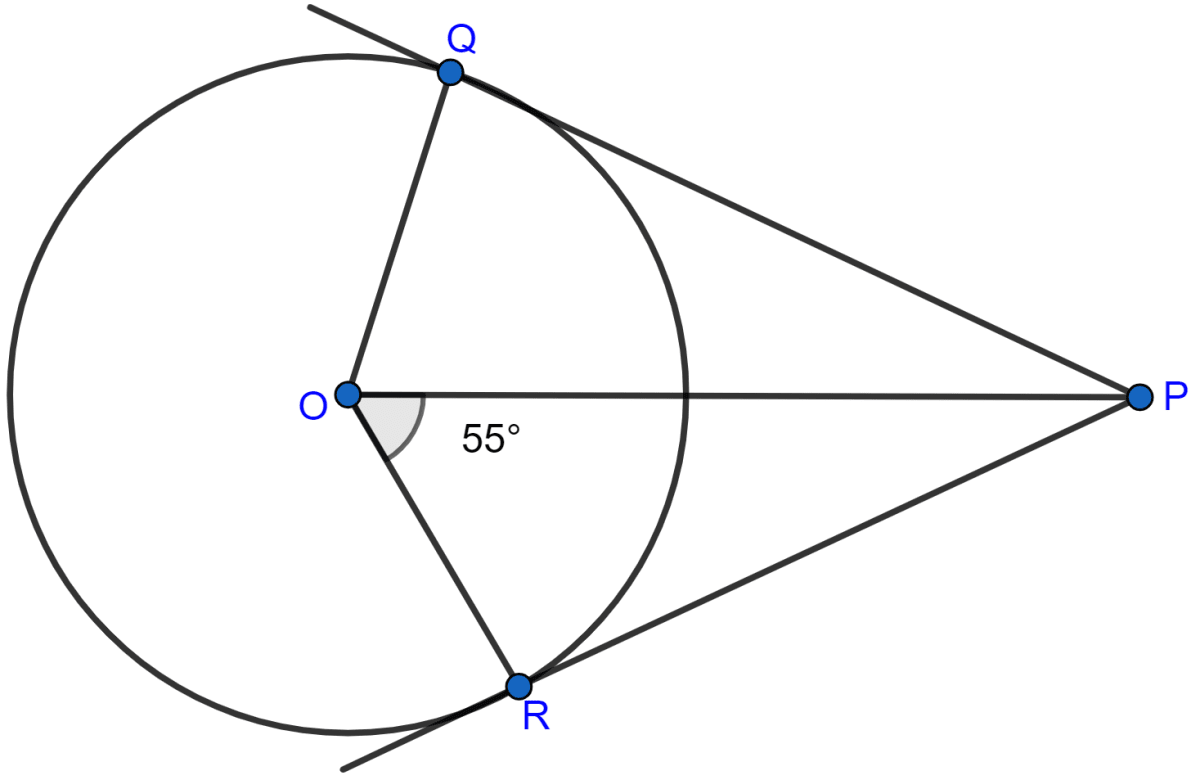
In the adjoining figure, PQ and PR are tangents from P to a circle with centre O. If ∠POR = 55°, then ∠QPR is
35°
55°
70°
80°
In the adjoining figure, PA and PB are tangents from point P to a circle with centre O. If the radius of the circle is 5 cm and PA ⊥ PB, then the length OP is equal to
5 cm
10 cm
7.5 cm
5√2 cm
