Mathematics
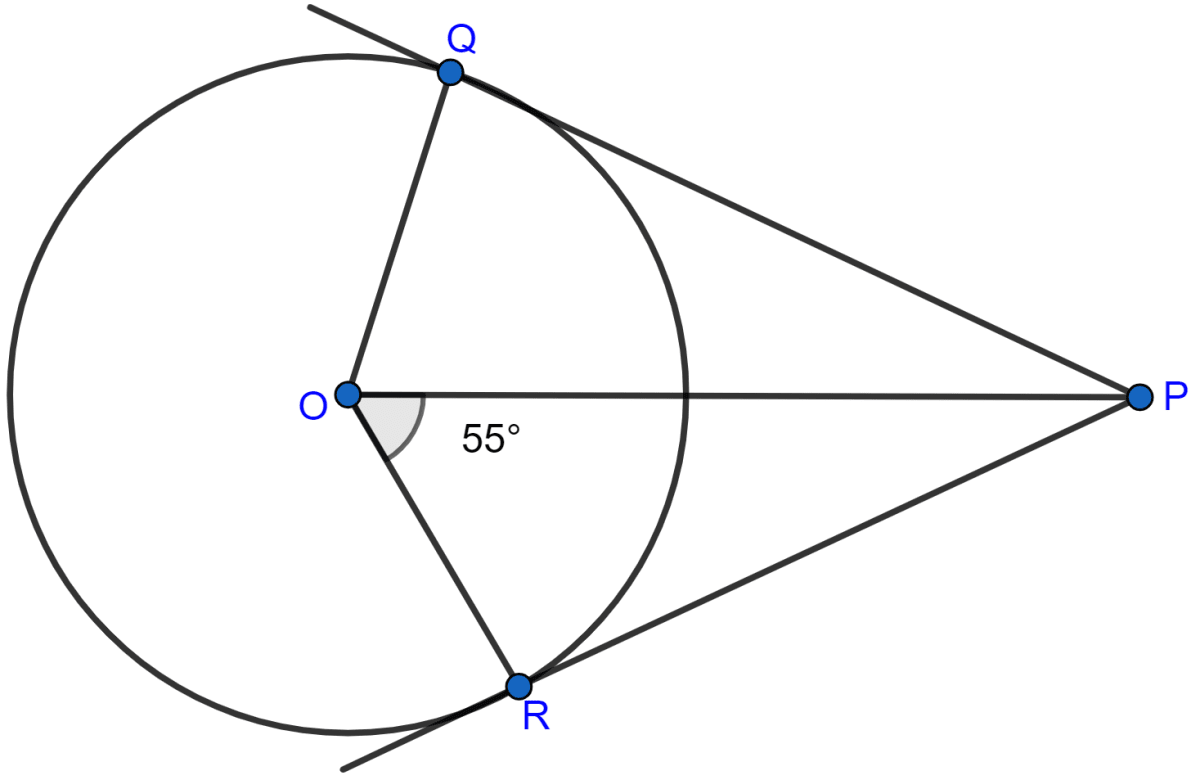
In the adjoining figure, PQ and PR are tangents from P to a circle with centre O. If ∠POR = 55°, then ∠QPR is
35°
55°
70°
80°
Circles
34 Likes
Answer
OR ⊥ PR (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ORP = 90°.
Since, sum of angles in a triangle = 180°.
⇒ ∠ORP + ∠POR + ∠OPR = 180°
⇒ 90° + 55° + ∠OPR = 180°
⇒ 145° + ∠OPR = 180°
⇒ ∠OPR = 180° - 145°
⇒ ∠OPR = 35°.
∠QPO = ∠OPR = 35° (∵ the tangents are equally inclined to the line joining the point and the centre of the circle.)
From figure,
∠QPR = ∠OPR + ∠QPO = 35° + 35° = 70°.
Hence, Option 3 is the correct option.
Answered By
24 Likes
Related Questions
In the adjoining figure, if O is the centre of the circle then the value of x is
18°
20°
24°
36°

From a point which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
60 cm2
65 cm2
30 cm2
32.5 cm2
In the adjoining figure, PA and PB are tangents from point P to a circle with centre O. If the radius of the circle is 5 cm and PA ⊥ PB, then the length OP is equal to
5 cm
10 cm
7.5 cm
5√2 cm

At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
4 cm
5 cm
6 cm
8 cm