Mathematics
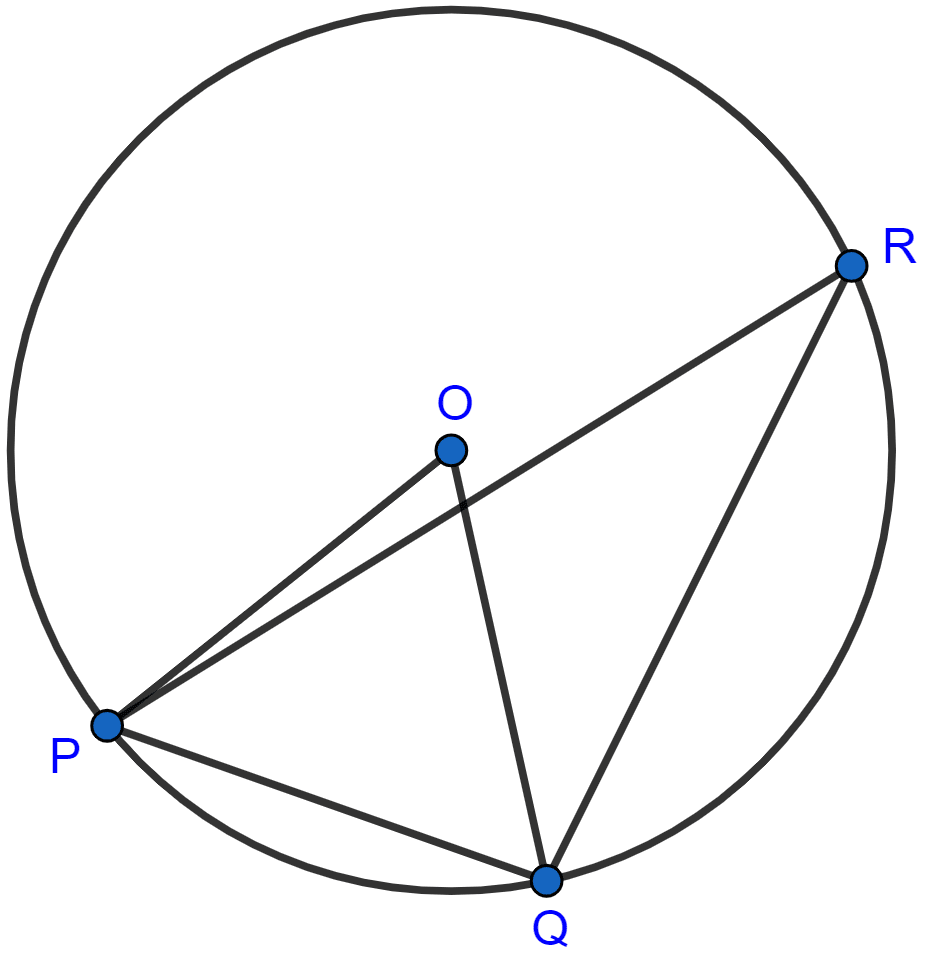
In the adjoining figure, O is the centre of the circle. If the length of the chord PQ is equal to the radius of the circle, then ∠PRQ is
60°
45°
30°
15°
Circles
12 Likes
Answer
From figure,
In △OPQ,
OP = OQ = PQ = (Radius of the circle.)
Hence, △OPQ is an equilateral triangle.
∴ ∠POQ = 60° (∵ all angles of an equilateral triangle = 60°.)
Arc PQ subtends ∠POQ at centre and ∠PRQ at remaining part of circle.
∠POQ = 2∠PRQ (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)
60° = 2∠PRQ
∠PRQ = = 30°.
Hence, Option 3 is the correct option.
Answered By
6 Likes
Related Questions
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
80°
50°
40°
30°
From a point which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
60 cm2
65 cm2
30 cm2
32.5 cm2
In the adjoining figure, if O is the centre of the circle then the value of x is
18°
20°
24°
36°

In the adjoining figure, O is the centre of the circle. If ∠BAO = 60°, then ∠ADC is equal to
30°
45°
60°
120°
