Mathematics
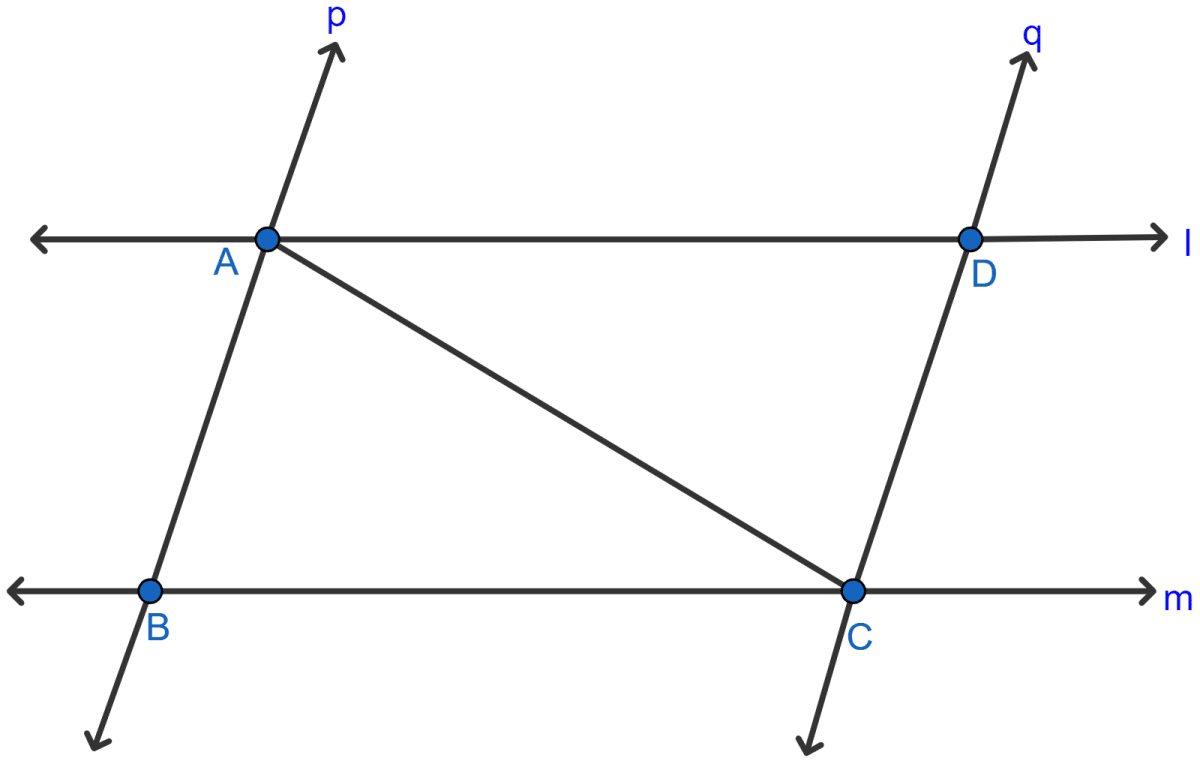
In the adjoining figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC ≅ △CDA.
Triangles
40 Likes
Answer
In △ABC and △CDA,
AC = AC (Common).
∠ACB = ∠CAD (Alternate angles)
∠BAC = ∠ACD (Alternate angles)
Hence, proved that △ABC ≅ △CDA by ASA axiom.
Answered By
29 Likes
Related Questions
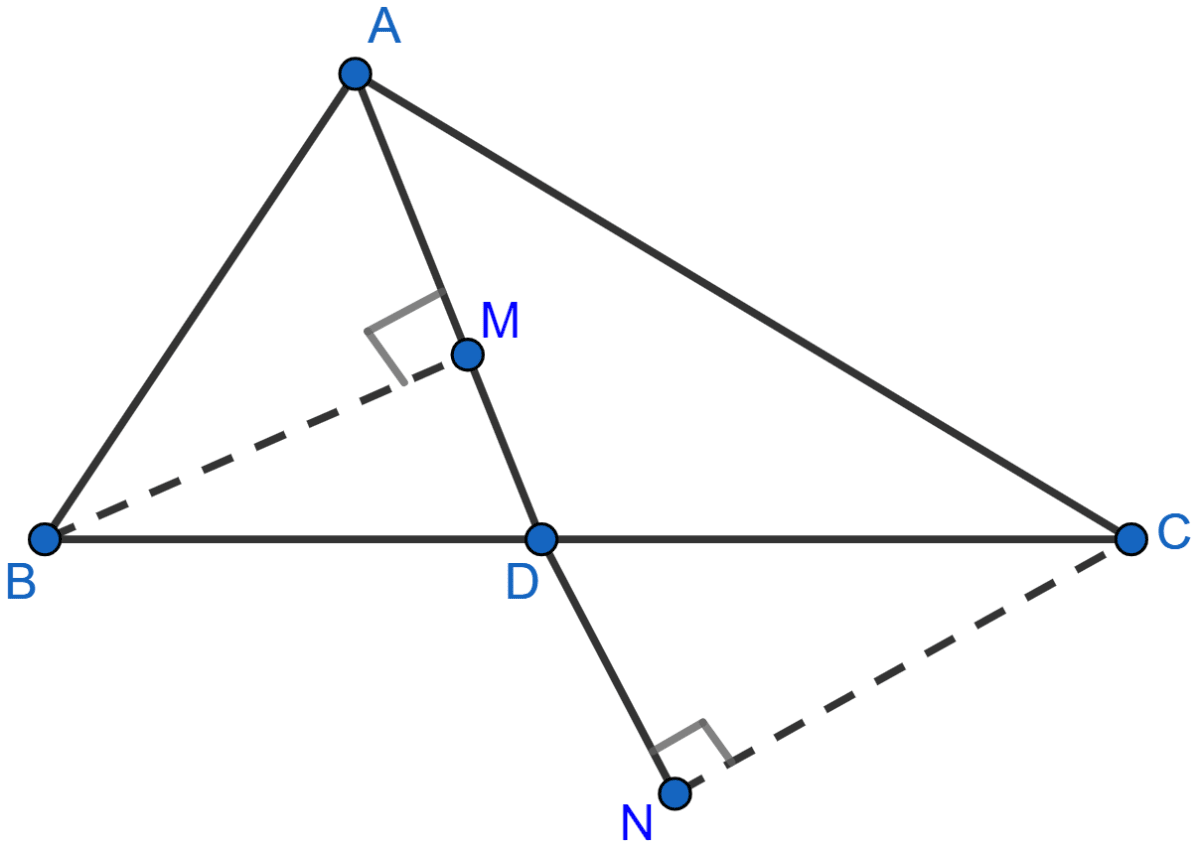
In the adjoining figure, AD is median of △ABC, BM and CN are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BM = CN.
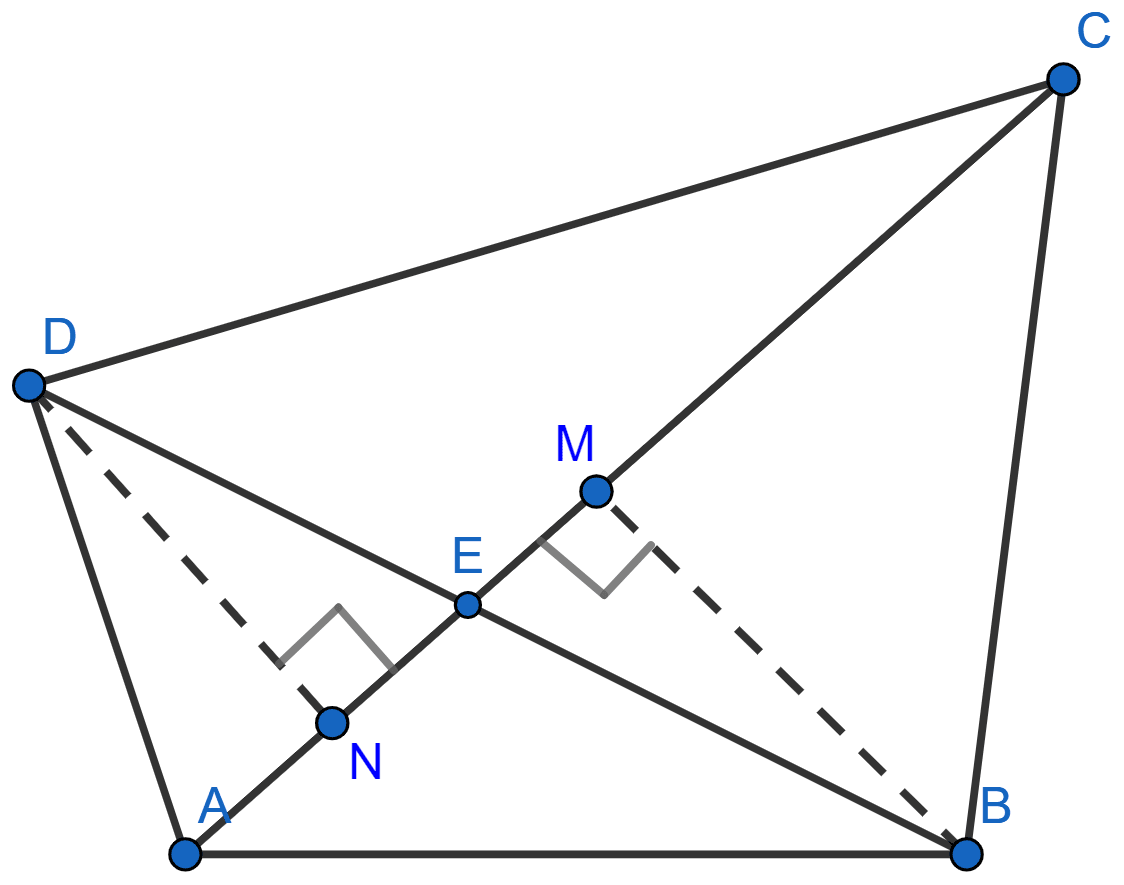
In the adjoining figure, BM and DN are perpendiculars to the line segment AC. If BM = DN, prove that AC bisects BD.
In the adjoining figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the mid-point of both the line segments AB and CD.

In the adjoining figure, ∠BCD = ∠ADC and ∠BCA = ∠ADB. Show that
(i) △ACD ≅ △BDC
(ii) BC = AD
(iii) ∠A = ∠B
