Mathematics
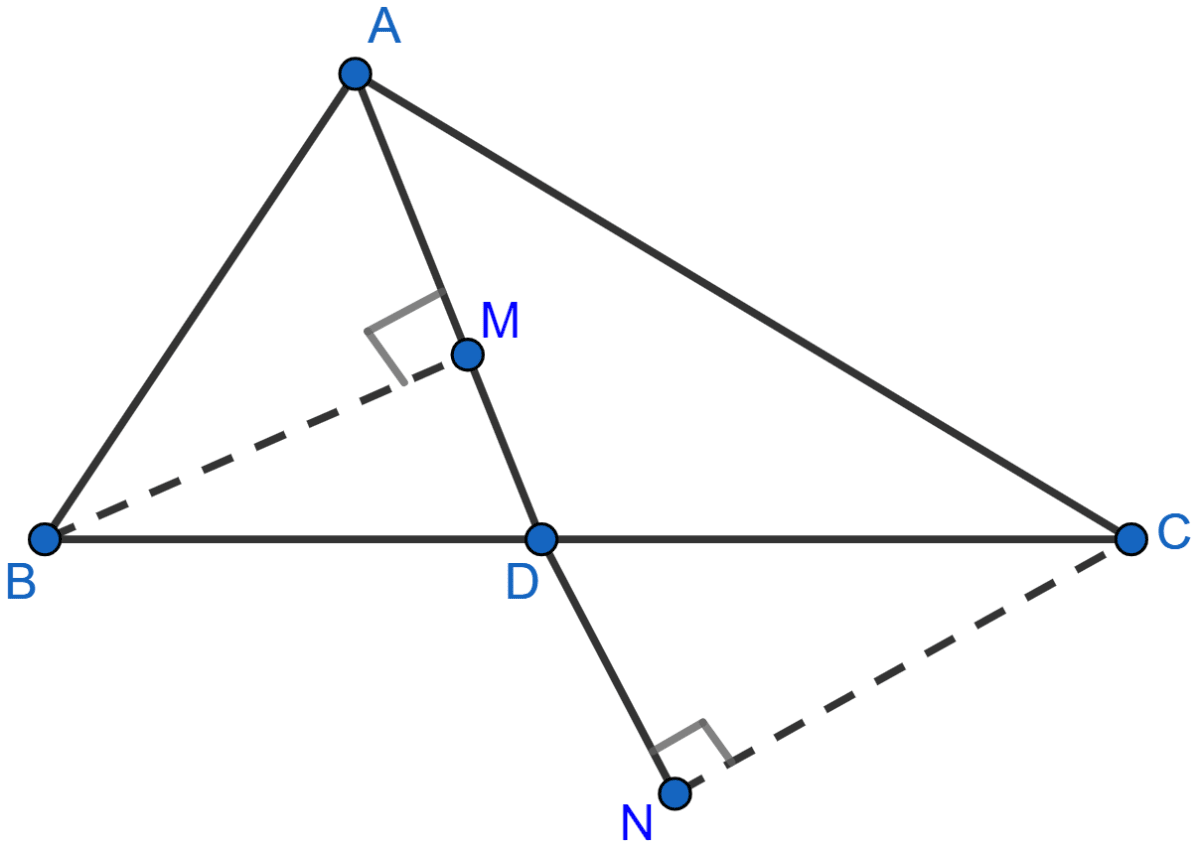
In the adjoining figure, AD is median of △ABC, BM and CN are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BM = CN.
Triangles
92 Likes
Answer
In △BMD and △CND,
BD = CD (As AD divides BC in two halves).
∠BMD = ∠CND (Both are equal to 90°)
∠BDM = ∠CDN (Vertically opposite angles)
∴ △BMD ≅ △CND by AAS axiom.
We know that corresponding sides of congruent triangles are equal.
∴ BM = CN.
Hence, proved that BM = CN.
Answered By
54 Likes
Related Questions
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side BC of △ABC so that the two triangles are congruent? Give reason for your answer.
"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent". Is the statement true? Why?
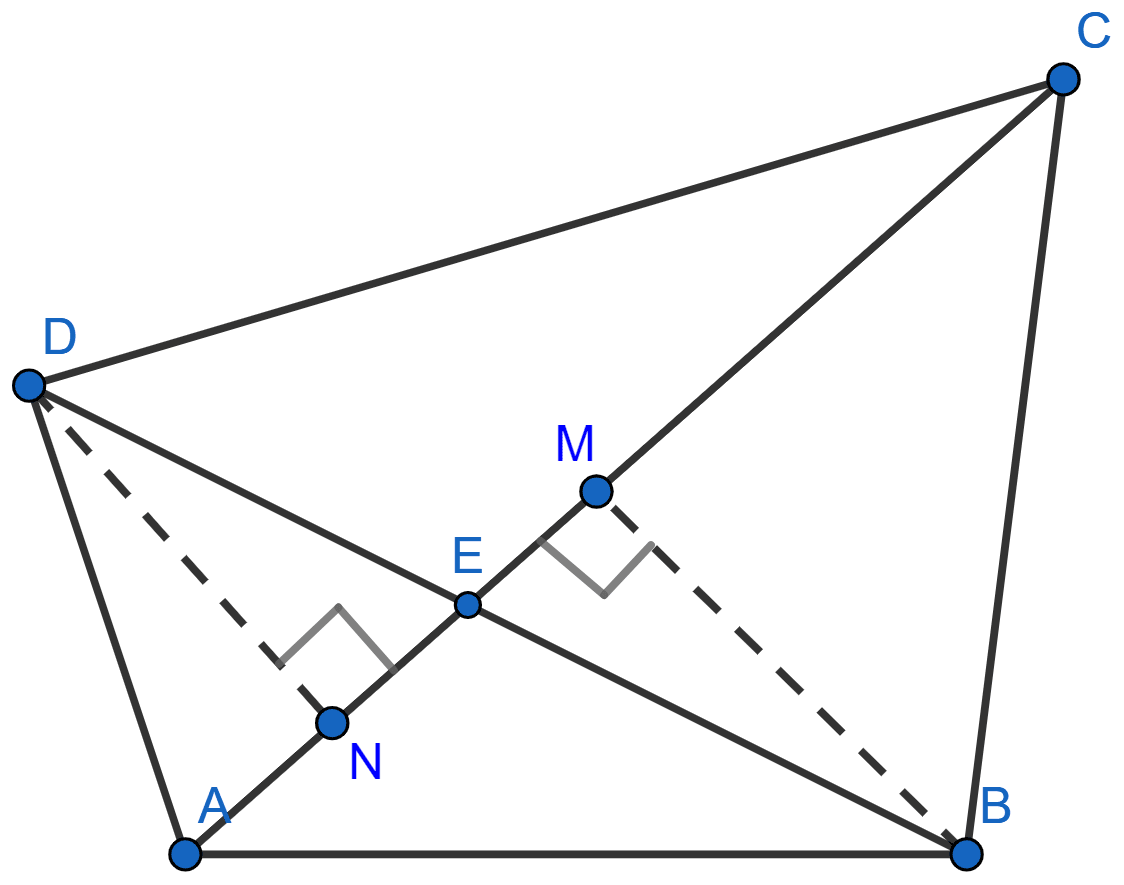
In the adjoining figure, BM and DN are perpendiculars to the line segment AC. If BM = DN, prove that AC bisects BD.
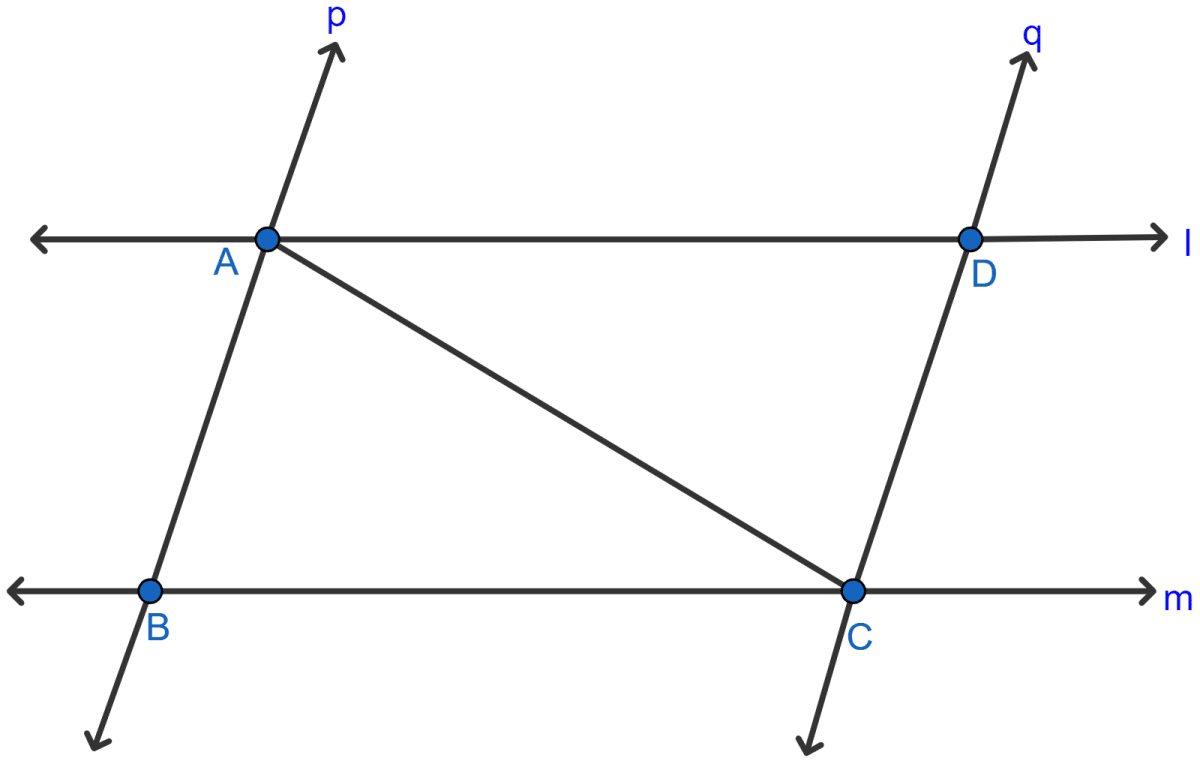
In the adjoining figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC ≅ △CDA.