Mathematics
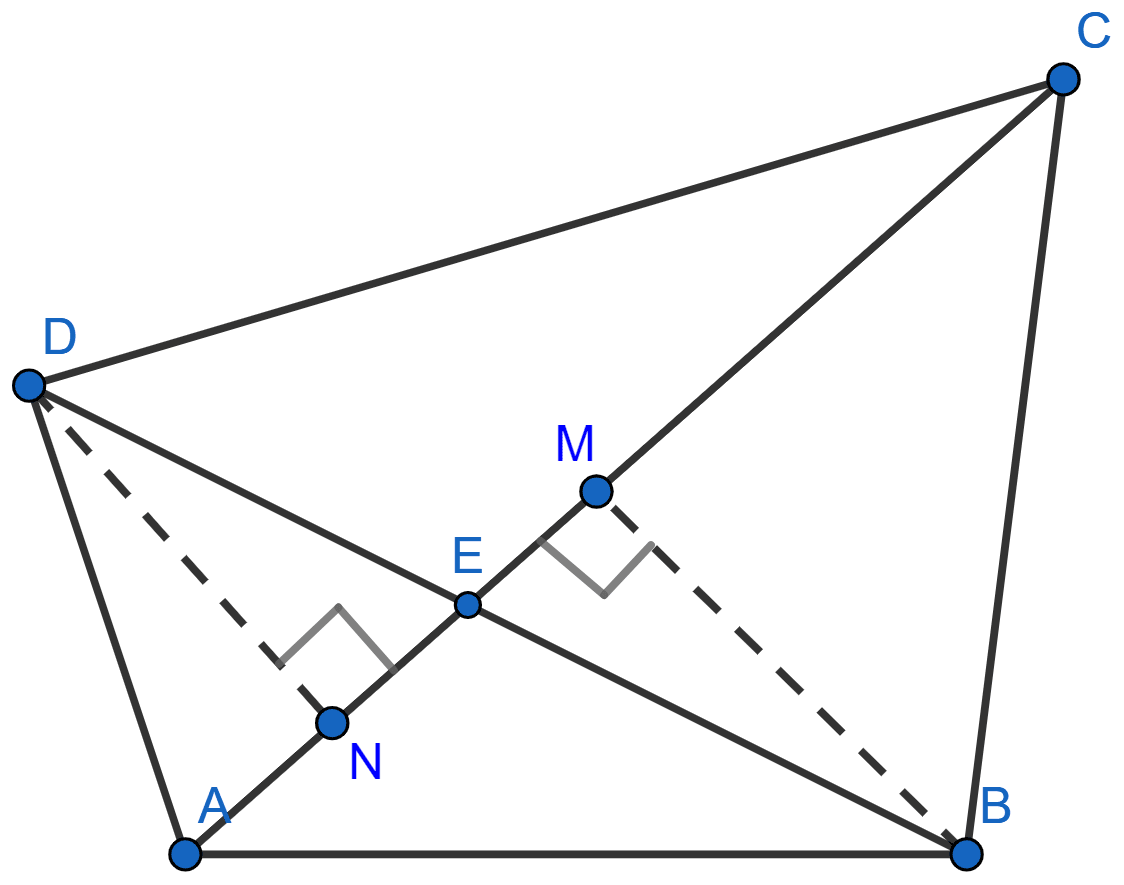
In the adjoining figure, BM and DN are perpendiculars to the line segment AC. If BM = DN, prove that AC bisects BD.
Triangles
57 Likes
Answer
In △BEM and △DEN,
BM = DN (Given).
∠BME = ∠DNE (Both are equal to 90°)
∠BEM = ∠DEN (Vertically opposite angles)
∴ △BEM ≅ △DEN by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ DE = BE.
Since, DE = BE it means that AC bisects BD at E.
Hence, proved that AC bisects BD.
Answered By
33 Likes
Related Questions
"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent". Is the statement true? Why?
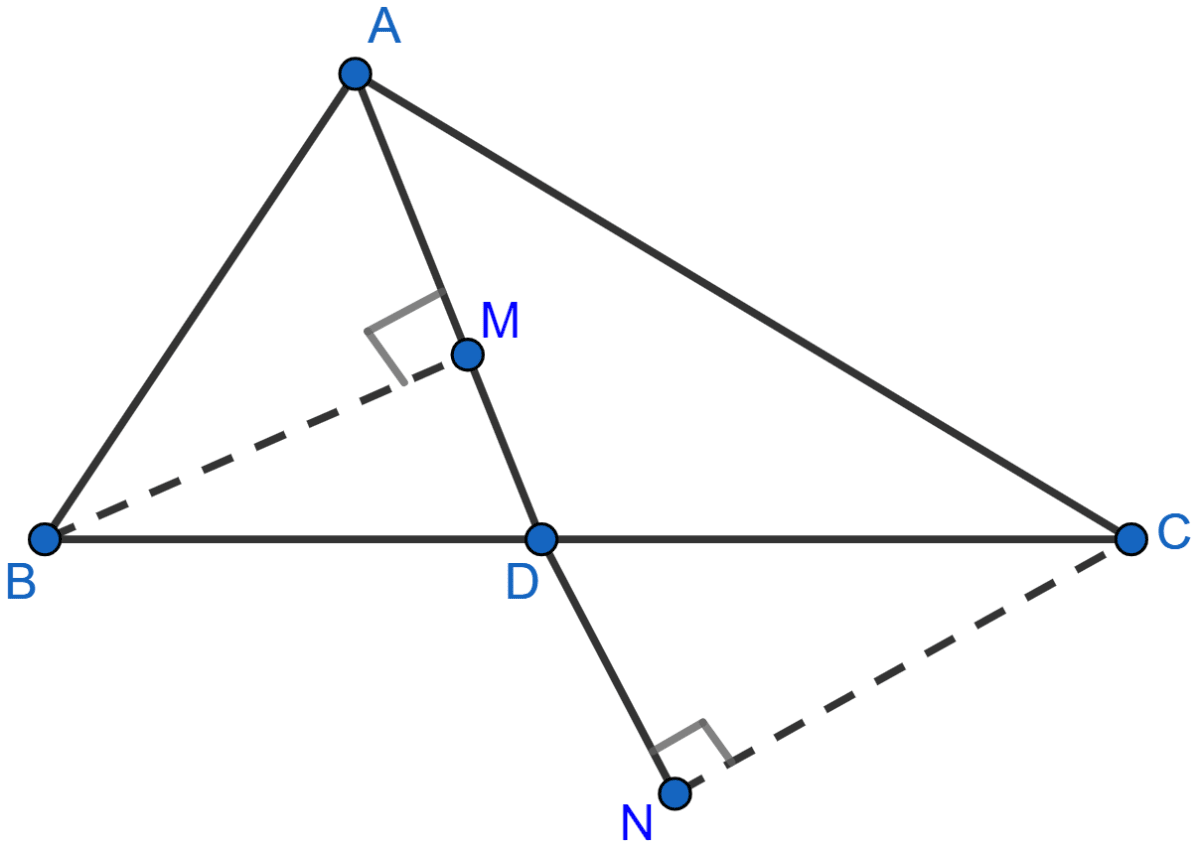
In the adjoining figure, AD is median of △ABC, BM and CN are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BM = CN.
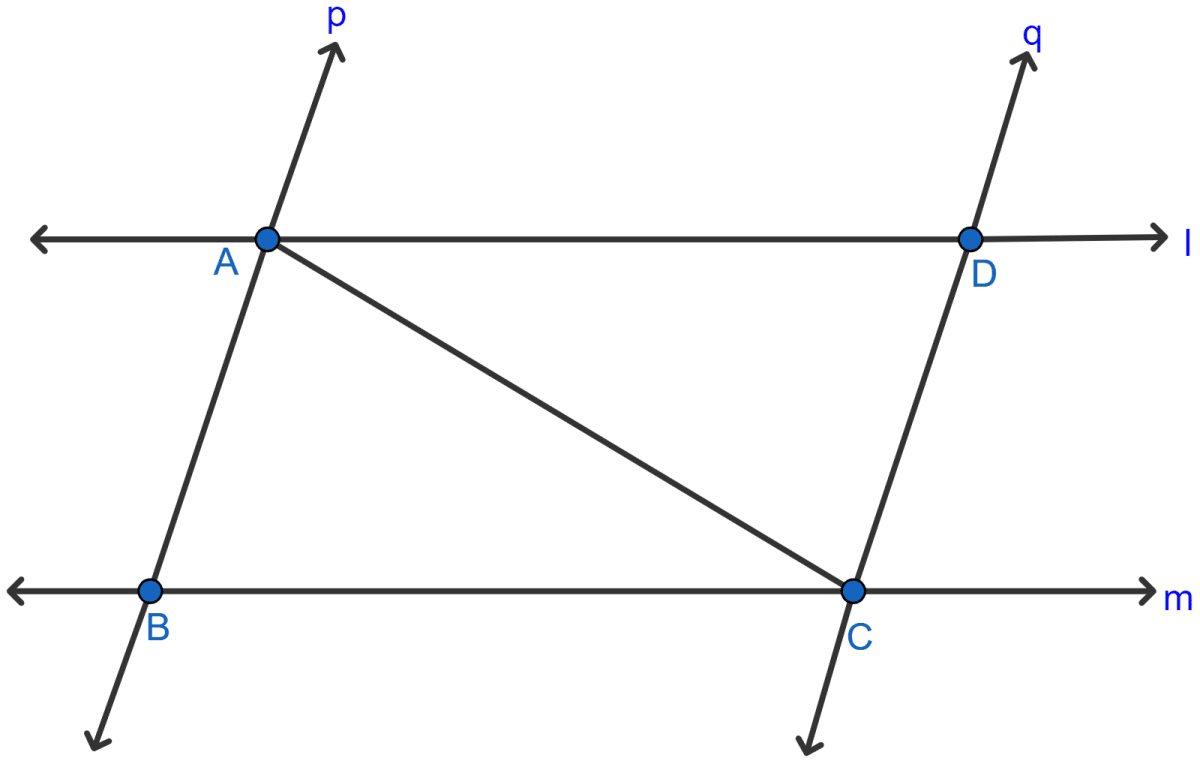
In the adjoining figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC ≅ △CDA.
In the adjoining figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the mid-point of both the line segments AB and CD.
