Mathematics
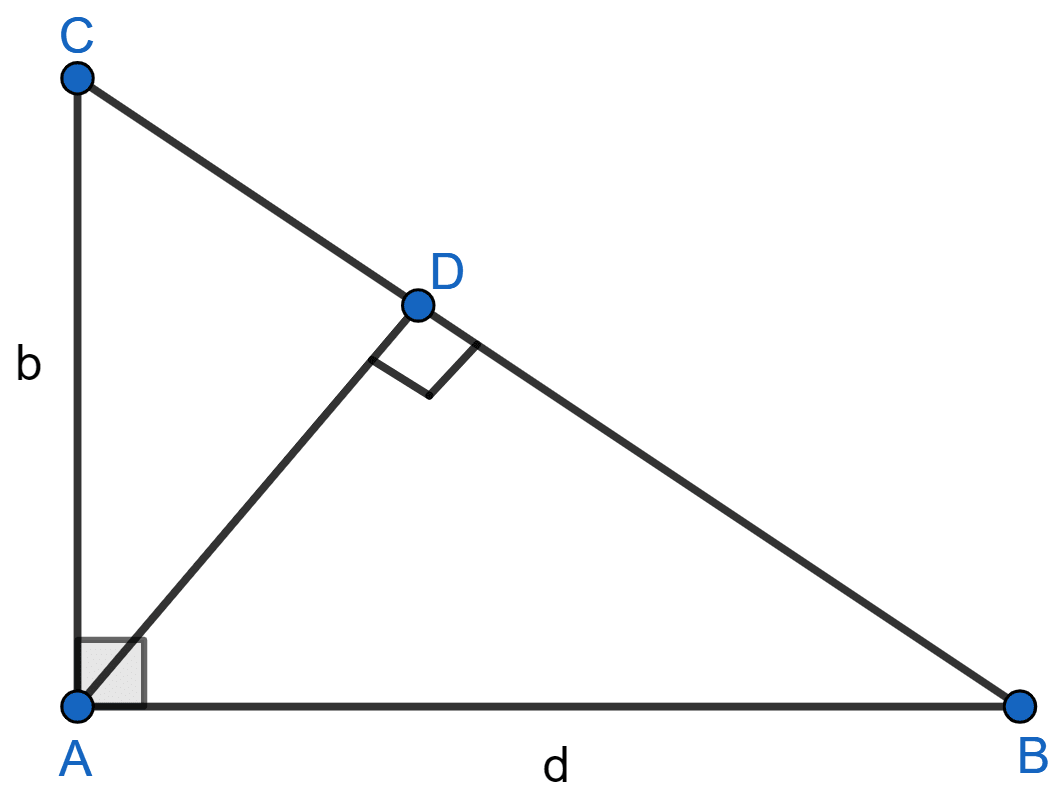
In the adjoining figure, find the length of AD in terms of b and c.
Pythagoras Theorem
46 Likes
Answer
In right angle triangle ABC,
By pythagoras theorem,
BC2 = AB2 + AC2
BC2 = c2 + b2
BC = .
From figure,
Area of △ABC = Area of △ABD + Area of △ADC
⇒ x AB x AC = x AD x BD + x AD x CD
⇒ (AB.AC) = (AD.BD + AD.CD)
⇒ AB.AC = AD.BD + AD.CD
⇒ AB.AC = AD(BD + CD)
⇒ AB.AC = AD.BC [∵ BD + CD = BC]
⇒ AD =
Putting values of AB, AC and BC in above equation we get,
AD =
Hence, AD = .
Answered By
34 Likes
Related Questions
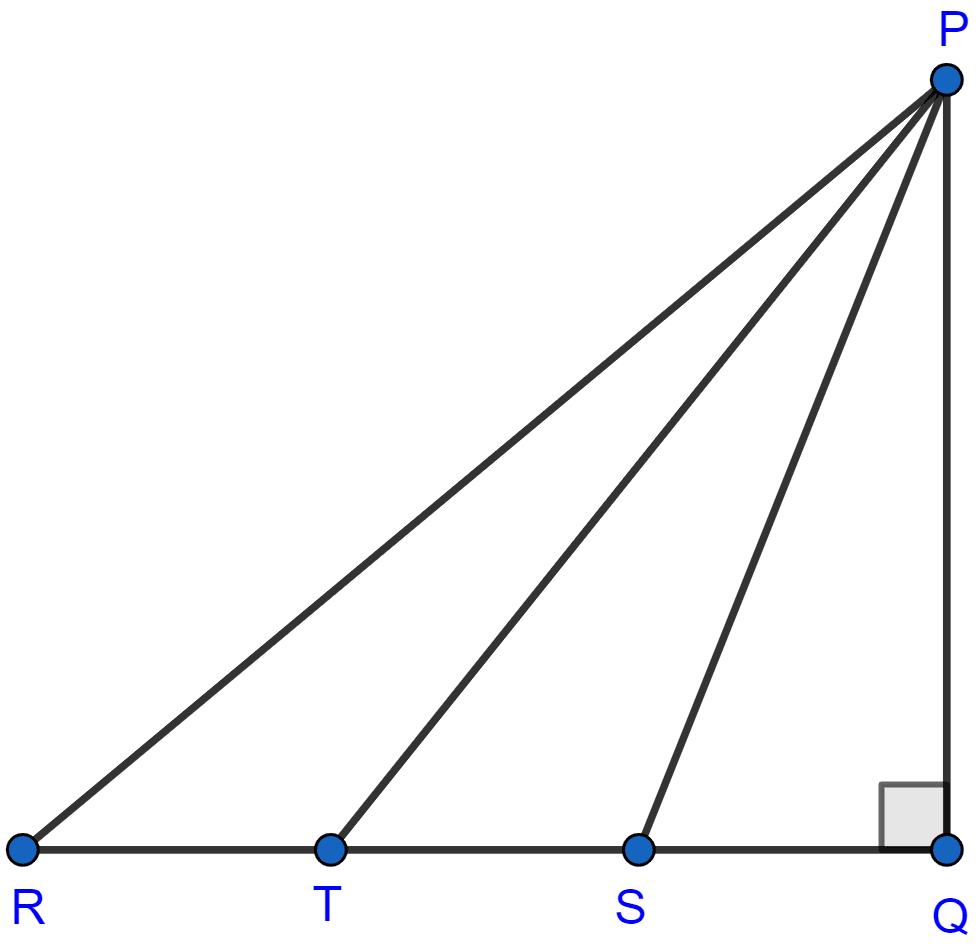
In the adjoining figure, △PQR is right angled at Q and points S and T trisect side QR. Prove that
8PT2 = 3PR2 + 5PS2.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2, Prove that ∠ACD = 90°.
ABCD is a square, F is mid-point of AB and BE is one third of BC. If area of △FBE is 108 cm2, find the length of AC.
In a triangle ABC, AB = AC and D is a point on side AC such that BC2 = AC × CD.
Prove that BD = BC.