Mathematics
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2, Prove that ∠ACD = 90°.
Pythagoras Theorem
8 Likes
Answer
In right angle triangle ABC,

By pythagoras theorem,
AC2 = AB2 + BC2 …….(i)
Given,
AD2 = AB2 + BC2 + CD2
Putting value of AB2 + BC2 from eqn (i) we get,
AD2 = AC2 + CD2
∴ △ACD is a right angled triangle.
In △ACD,
∠ACD = 90° i.e. angle opposite to hypotenuse = 90° (By converse of pythagoras theorem.)
Hence, proved that ∠ACD = 90°.
Answered By
7 Likes
Related Questions
In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that
(i) 9AQ2 = 9AC2 + 4BC2
(ii) 9BP2 = 9BC2 + 4AC2
(iii) 9(AQ2 + BP2) = 13AB2
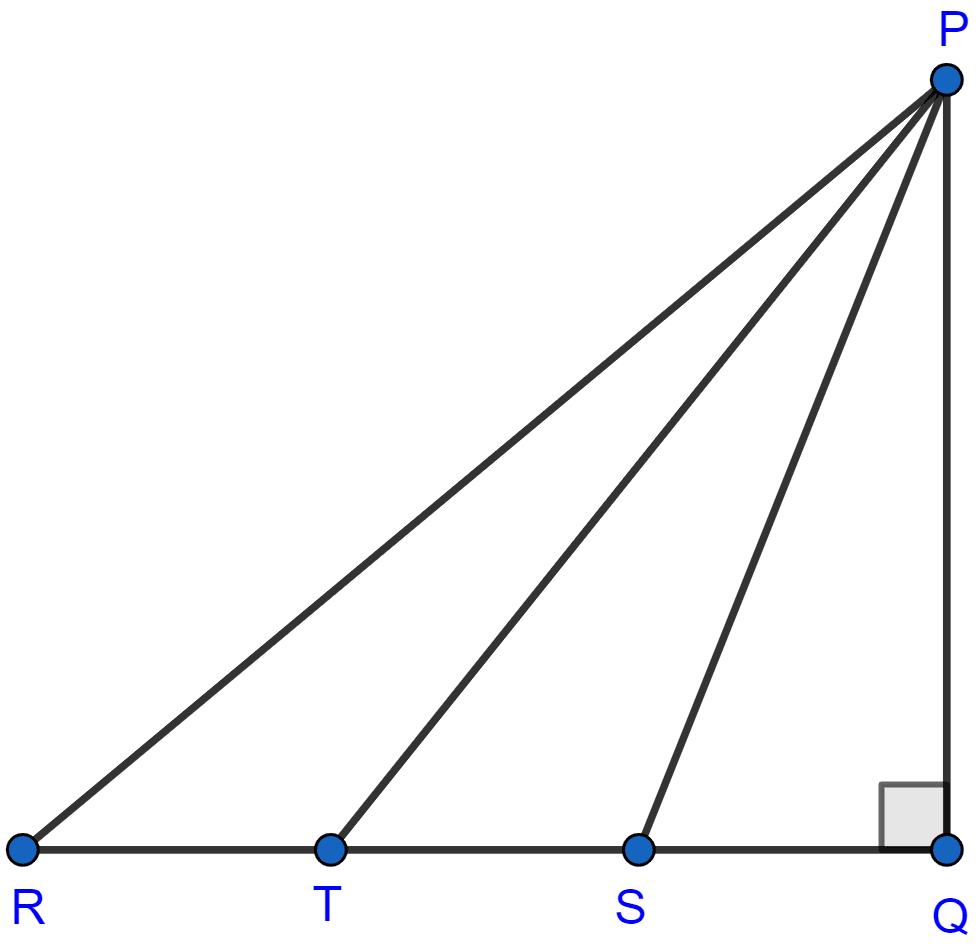
In the adjoining figure, △PQR is right angled at Q and points S and T trisect side QR. Prove that
8PT2 = 3PR2 + 5PS2.
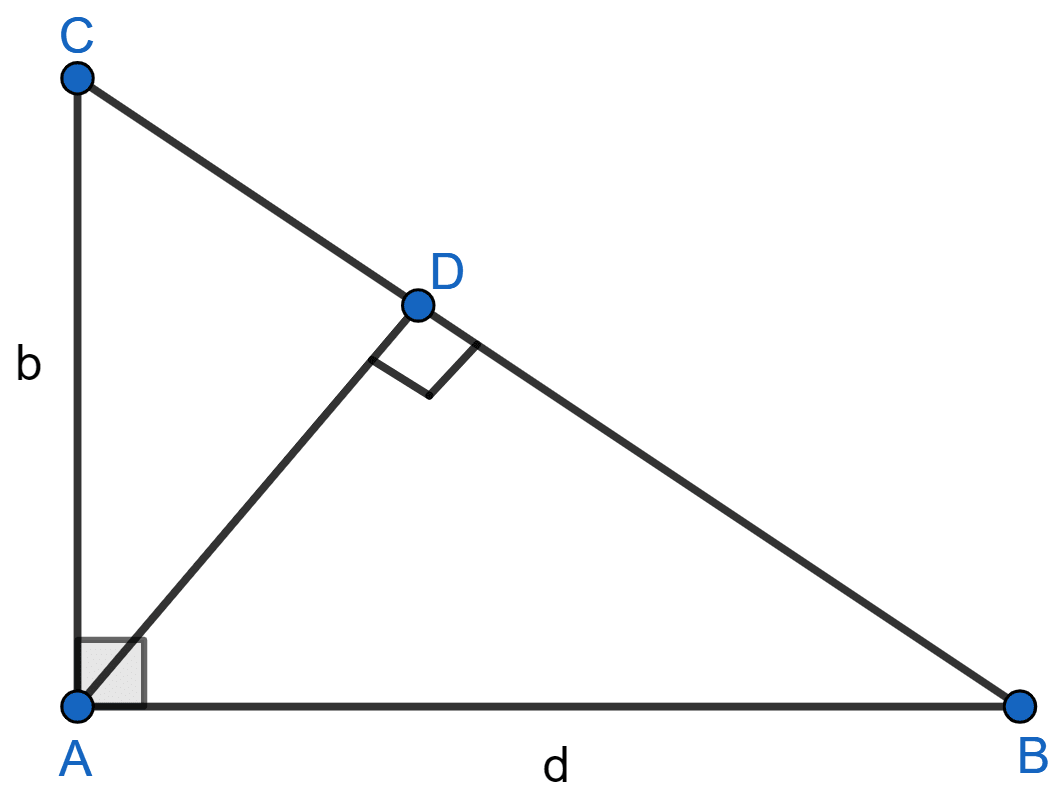
In the adjoining figure, find the length of AD in terms of b and c.
ABCD is a square, F is mid-point of AB and BE is one third of BC. If area of △FBE is 108 cm2, find the length of AC.