Mathematics
In a triangle ABC, AB = AC and D is a point on side AC such that BC2 = AC × CD.
Prove that BD = BC.
Pythagoras Theorem
44 Likes
Answer
Draw BE ⊥ AC.

In right triangle BEC,
By pythagoras theorem,
⇒ BC2 = BE2 + EC2
⇒ BC2 = BE2 + (AC - AE)2
⇒ BC2 = BE2 + AC2 + AE2 - 2AC.AE ………(i)
In right triangle ABE,
By pythagoras theorem,
⇒ AB2 = BE2 + AE2………(ii)
Substituting value of BE2 + AE2 from (ii) in (i) we get,
⇒ BC2 = AB2 + AC2 - 2AC.CE
⇒ BC2 = AC2 + AC2 - 2AC.AE [∵ AB = AC]
⇒ BC2 = 2AC2 - 2AC.AE
⇒ BC2 = 2AC(AC - AE)
⇒ BC2 = 2AC × EC ………(iii)
Given, BC2 = AC × CD ……….(iv)
Comparing (iii) and (iv) we get,
⇒ 2AC × EC = AC × CD
⇒ 2EC = CD or EC =
So, we can say that ED = EC as E is mid-point of CD.
In △BDE and △BCE,
BE = BE (Common)
ED = EC
∠BED = ∠BEC = 90°
△BDE ≅ △BCE by SAS axiom of congruency.
We know that corresponding parts of congruent triangle are equal.
∴ BD = BC.
Hence, proved that BD = BC.
Answered By
32 Likes
Related Questions
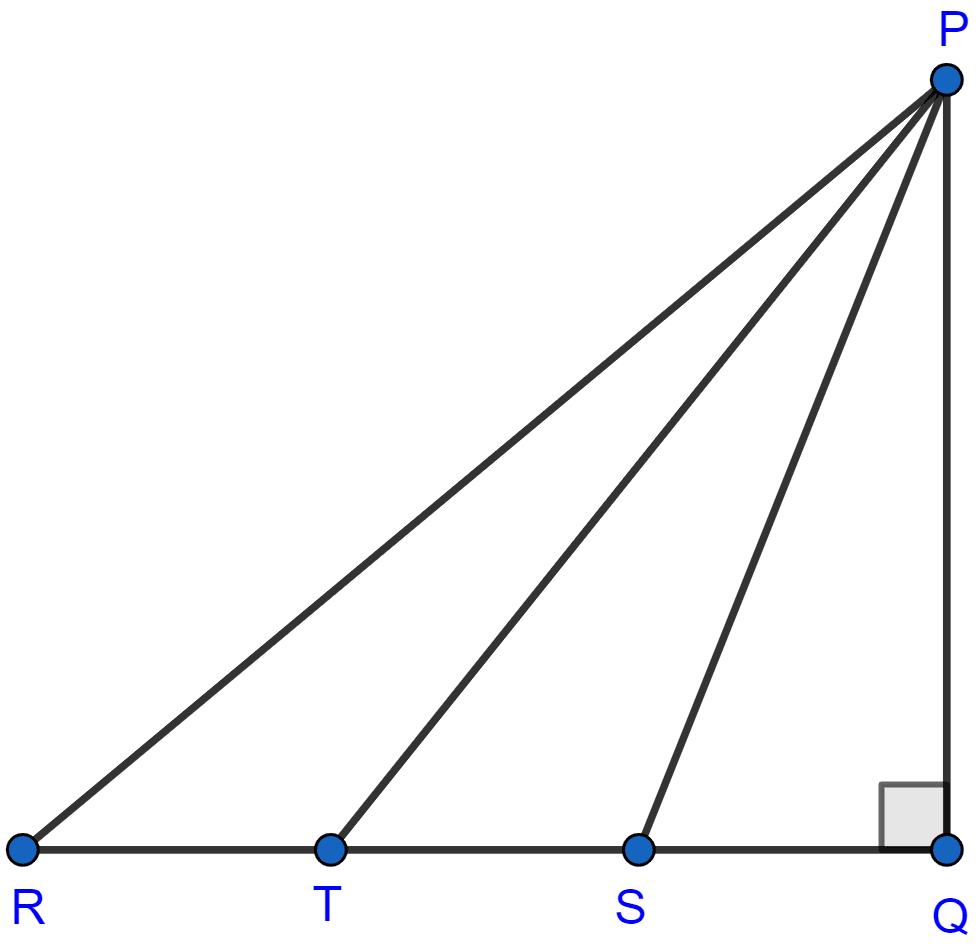
In the adjoining figure, △PQR is right angled at Q and points S and T trisect side QR. Prove that
8PT2 = 3PR2 + 5PS2.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2, Prove that ∠ACD = 90°.
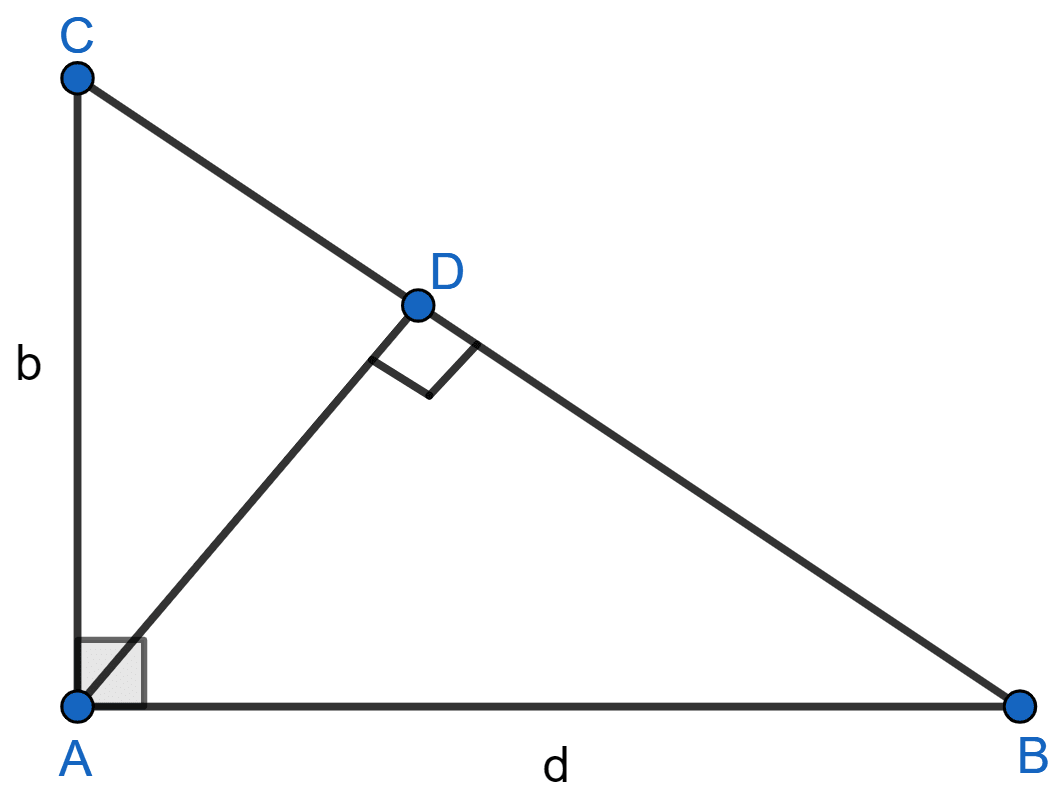
In the adjoining figure, find the length of AD in terms of b and c.
ABCD is a square, F is mid-point of AB and BE is one third of BC. If area of △FBE is 108 cm2, find the length of AC.