Mathematics
In the adjoining figure, D, E and F are midpoints of the sides BC, CA and AB respectively of ∆ABC. Prove that BCEF is a trapezium and area of the trap. BCEF = area of ∆ABC.

Theorems on Area
38 Likes
Answer
We know that D and E are the mid-points of BC and CA, respectively.
By mid-point theorem,
DE || AB and DE = AB = BF (As F is mid-point of AB)
From figure,
BF || DE and BF = DE.
Hence, BDEF is a || gm.
Similarly,
F and E are the mid-points of AB and CA.
By mid-point theorem,
EF || BC and EF = BC = DC (As D is mid-point of BC)
From figure,
EF || DC and EF = DC.
Hence, EFDC is a || gm.
Since, FE || BC and FB, EC are not parallel.
Hence, EFBC is a trapezium.
F and D are the mid-points of AB and BC.
By mid-point theorem,
FD || AC and FD = AC = AE (As E is mid-point of AC)
From figure,
FD || AE and FD = AE.
Hence, AFDE is a || gm.
We know that a diagonal divides a || gm in two triangles of equal area.
In || gm BDEF, FD is the diagonal,
∴ area of △DEF = area of △BDF ………(i)
In || gm EFDC, DE is the diagonal,
∴ area of △DEF = area of △EDC ………(ii)
In || gm AFDE, FE is the diagonal,
∴ area of △DEF = area of △AFE ………(iii)
From (i), (ii) and (iii) we get,
area of △DEF = area of △BDF = area of △EDC = area of △AFE …….(iv)
From figure,
area of △ABC = area of △DEF + area of △BDF + area of △EDC + area of △AFE
= area of △DEF + area of △DEF + area of △DEF + area of △DEF
= 4 x area of △DEF
∴ area of △ABC = 4 x area of △DEF
⇒ area of △DEF = area of △ABC ……(v)
From figure,
area of trapezium BCEF = area of △DEF + area of △BDF + area of △EDC
= area of △DEF + area of △DEF + area of △DEF
= 3 x area of △DEF
∴ area of trapezium BCEF = 3 x area of △DEF
⇒ area of △DEF = x area of trapezium BCEF …….(vi)
From (v) and (vi) we get,
⇒ area of △ABC = area of trapezium BCEF
⇒ area of trapezium BCEF = area of △ABC.
Hence, proved that area of trapezium BCEF = area of △ABC.
Answered By
24 Likes
Related Questions
In the figure (2) given below, PQRS and ABRS are parallelograms, and X is any point on the side BR. Show that
area of ∆AXS = area of || gm PQRS.

D, E and F are mid-points of the sides BC, CA and AB respectively of a ∆ABC. Prove that
(i) FDCE is a parallelogram
(ii) area of ∆DEF = area of ∆ABC
(iii) area of || gm FDCE = area of ∆ABC
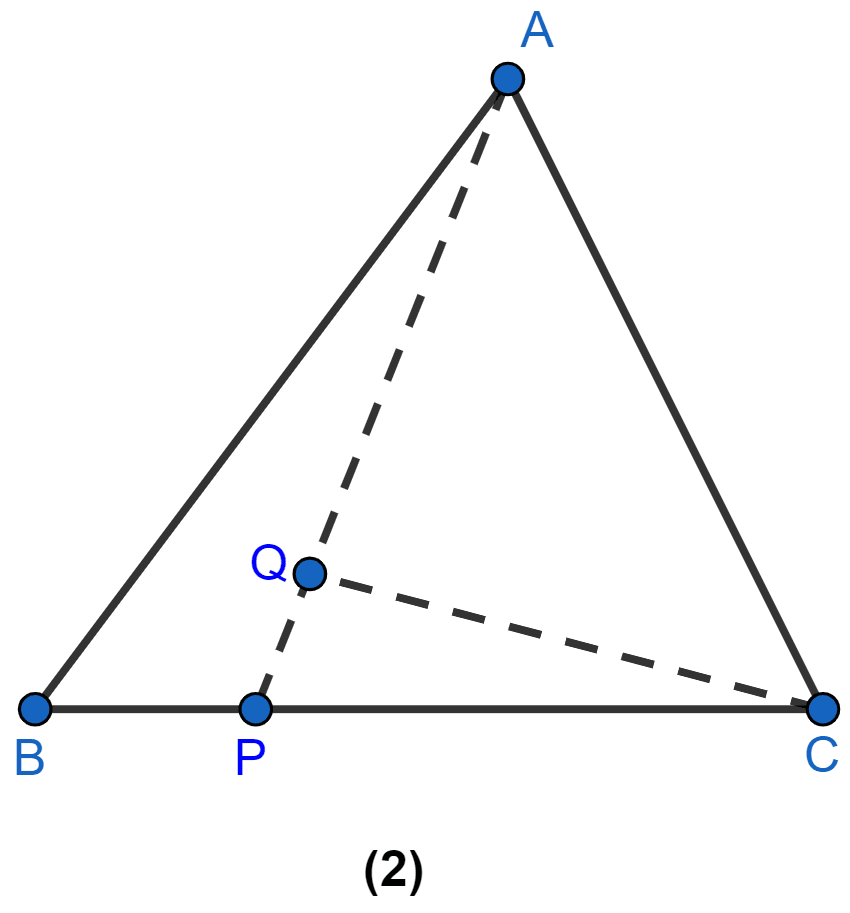
In figure (1) given below, point D divides the side BC of ∆ABC in the ratio m : n. Prove that area of ∆ABD : area of ∆ADC = m : n.
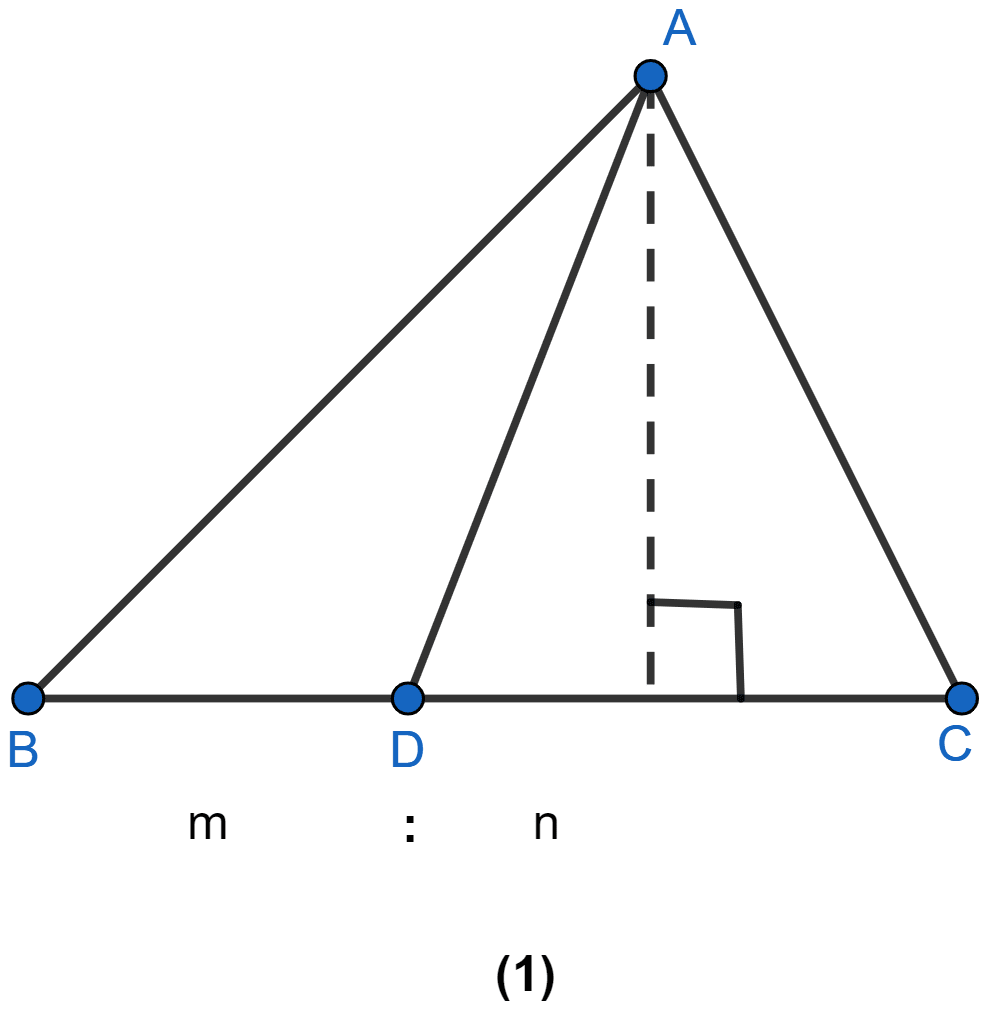
In the figure (2) given below, P is a point on the side BC of ∆ABC such that PC = 2BP, and Q is a point on AP such that QA = 5PQ, find area of ∆AQC : area of ∆ABC.