Mathematics
In the adjoining figure, ∠BCD = ∠ADC and ∠BCA = ∠ADB. Show that
(i) △ACD ≅ △BDC
(ii) BC = AD
(iii) ∠A = ∠B

Answer
(i) In △ACD and △BDC,
Given,
∠BCD = ∠ADC
∠BCA = ∠ADB
∴ ∠BCD + ∠BCA = ∠ADC + ∠ADB
⇒ ∠ACD = ∠BDC
CD = CD (Common).
∠ADC = ∠BCD (Given)
Hence, proved that △ACD ≅ △BDC by ASA axiom.
(ii) We know that, △ACD ≅ △BDC.
We know that corresponding sides of congruent triangles are equal.
∴ BC = AD.
Hence, proved that BC = AD.
(iii) We know that, △ACD ≅ △BDC.
We know that corresponding angles of congruent triangles are equal.
∴ ∠A = ∠B.
Hence, proved that ∠A = ∠B.
Related Questions
In the adjoining figure, ∠ABC = ∠ACB, D and E are points on the sides AC and AB respectively such that BE = CD. Prove that
(i) △EBC ≅ △DCB
(ii) △OEB ≅ △ODC
(iii) OB = OC.

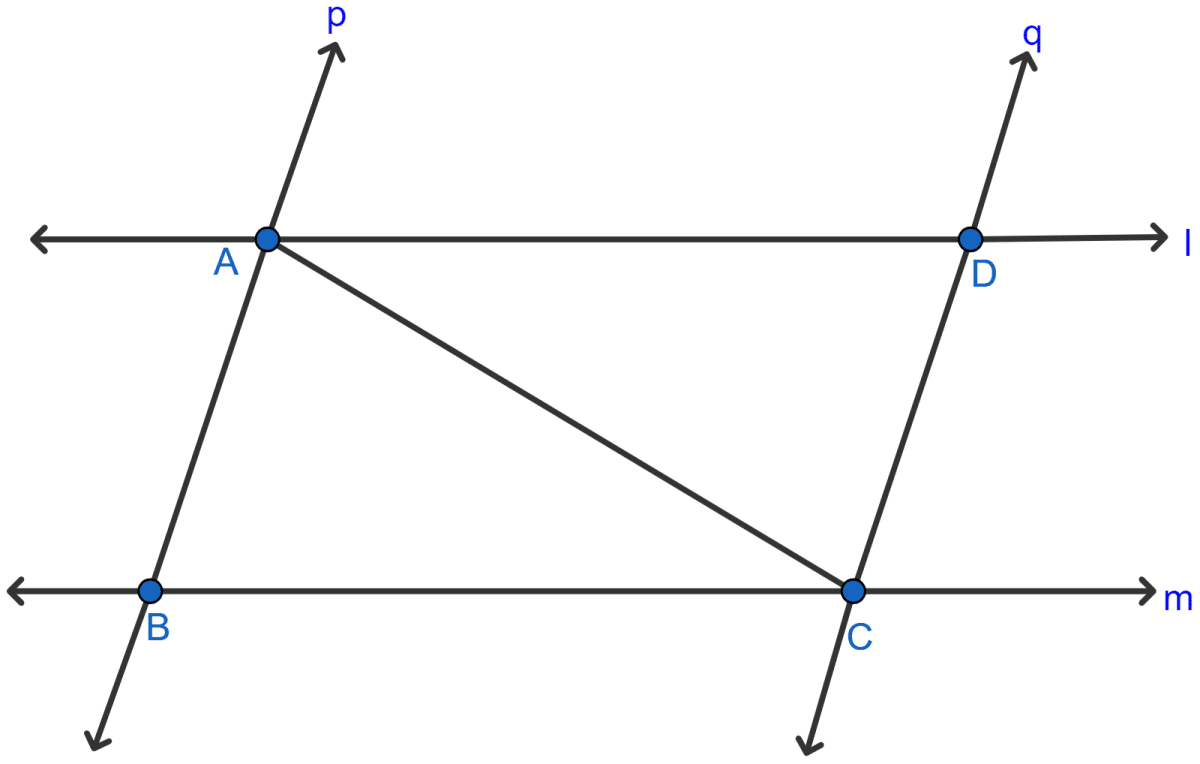
In the adjoining figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC ≅ △CDA.
In the adjoining figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the mid-point of both the line segments AB and CD.

ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.