Mathematics
In the adjoining figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that △ABC ≅ △DEF.

Related Questions
In the adjoining figure, ∠ABC = ∠ACB, D and E are points on the sides AC and AB respectively such that BE = CD. Prove that
(i) △EBC ≅ △DCB
(ii) △OEB ≅ △ODC
(iii) OB = OC.

ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
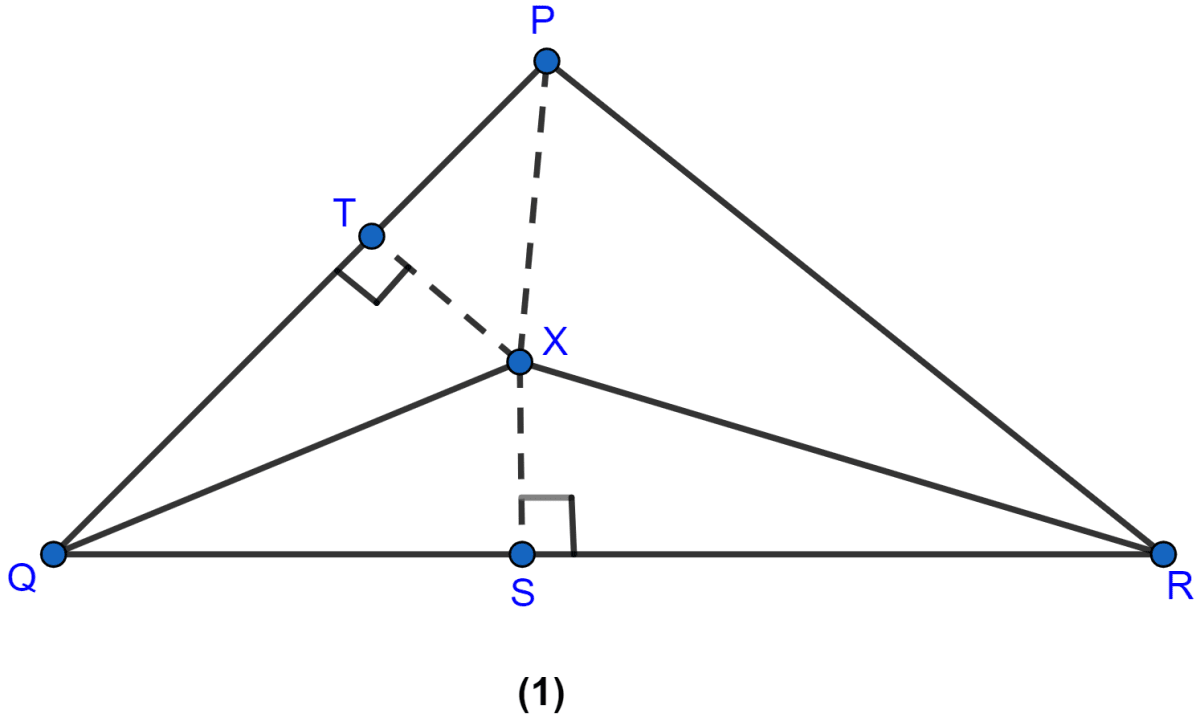
In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of △PQR. If XS ⊥ QR and XT ⊥ PQ, prove that
(i) △XTQ ≅ △XSQ
(ii) PX bisects the angle P.