Mathematics
In the adjoining figure, △ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of △ABC is parallel to BC.
Circles
31 Likes
Answer
In △ABC,
AB = AC (Given)
∴ ∠C = ∠B (∵ angles opposite to equal sides are equal.)
From figure,
∠TAC = ∠B (∵ angles in alternate segment are equal.)
But ∠B = ∠C
∴ ∠TAC = ∠C
But angles ∠TAC and ∠C are alternate angles. Since, they are equal
Hence, proved that AT || BC.
Answered By
19 Likes
Related Questions
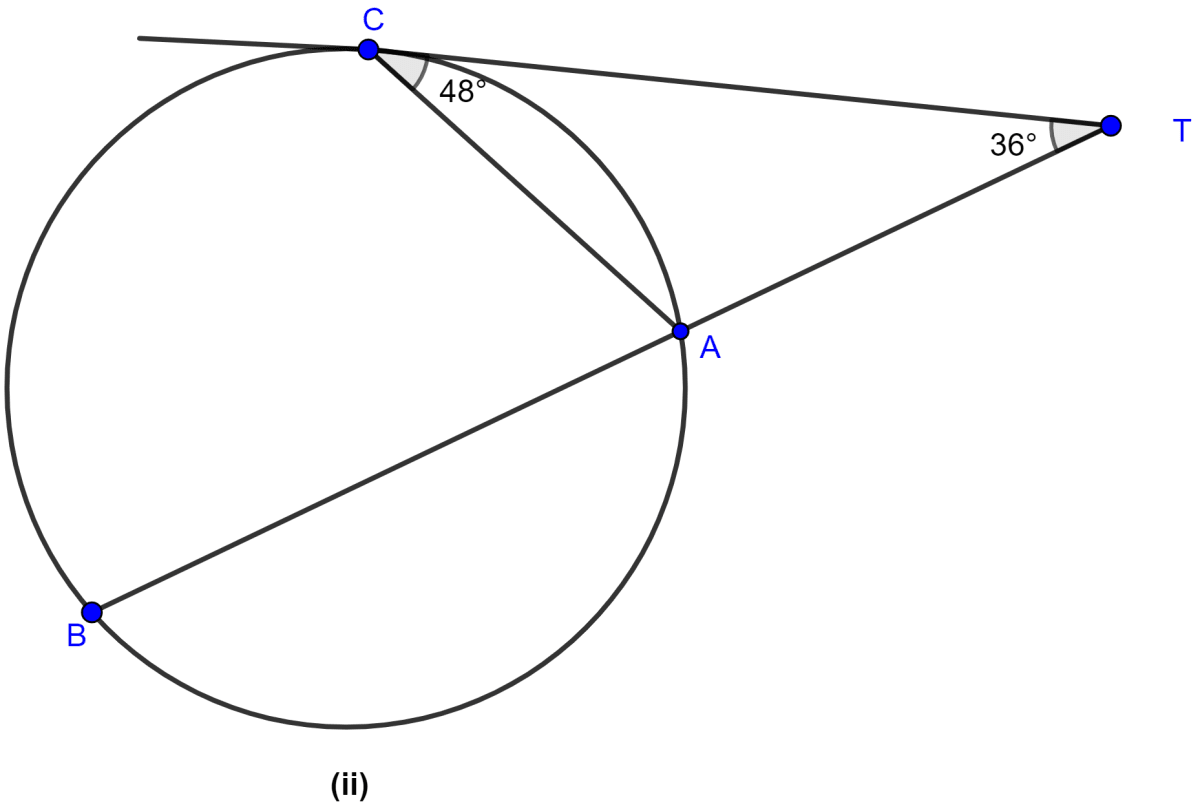
In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.
In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.
