Mathematics
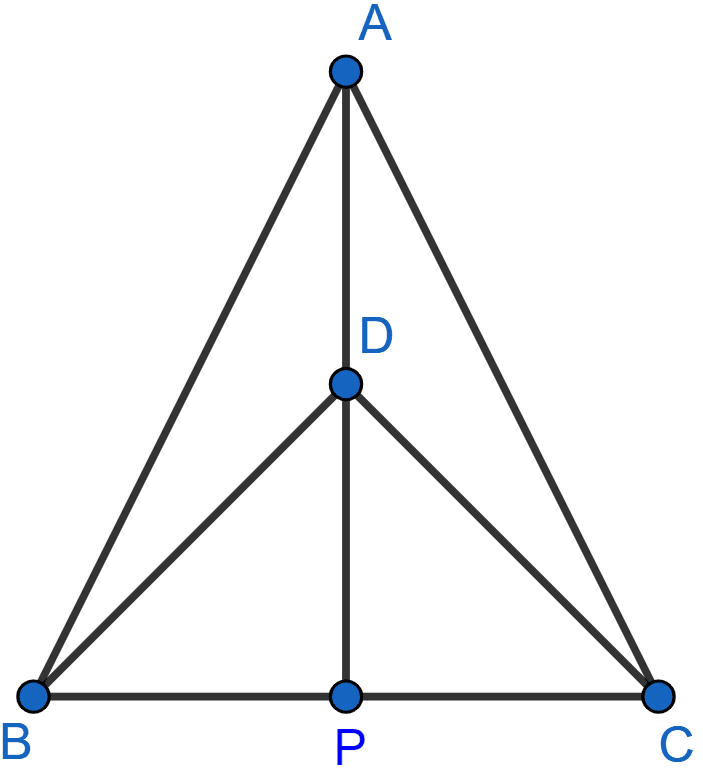
In the adjoining figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Answer
(i) AB = AC (as ABC is an isosceles triangle on base BC)
DB = DC (as DBC is an isosceles triangle on base BC)
AD = AD (Common)
∴ △ABD ≅ △ACD by SSS axiom.
Hence, proved that △ABD ≅ △ACD.
(ii) AB = AC (as ABC is an isosceles triangle on base BC)
AP = AP (Common)
∠ABP = ∠ACP (As angles opposite to equal sides are equal.)
∴ △ABP ≅ △ACP by AAS axiom.
Hence, proved that △ABP ≅ △ACP.
(iii) We know that,
△ABP ≅ △ACP.
As corresponding parts of congruent triangle are equal.
∴ ∠BAP = ∠CAP ……(i)
also ∠APB = ∠APC.
△DPB ≅ △DPC (By SAS axiom)
As corresponding parts of congruent triangle are equal.
∴ ∠BDP = ∠CDP ……(ii)
From (i) and (ii) we can say that AP bisects ∠A as well as ∠D.
Hence, proved that AP bisects ∠A as well as ∠D.
(iv) Since, ∠BPA = ∠CPA.
From figure,
∠BPA + ∠CPA = 180°
2∠BPA = 180°
∠BPA = 90°.
Hence, proved that AP is the perpendicular bisector of BC.