Mathematics
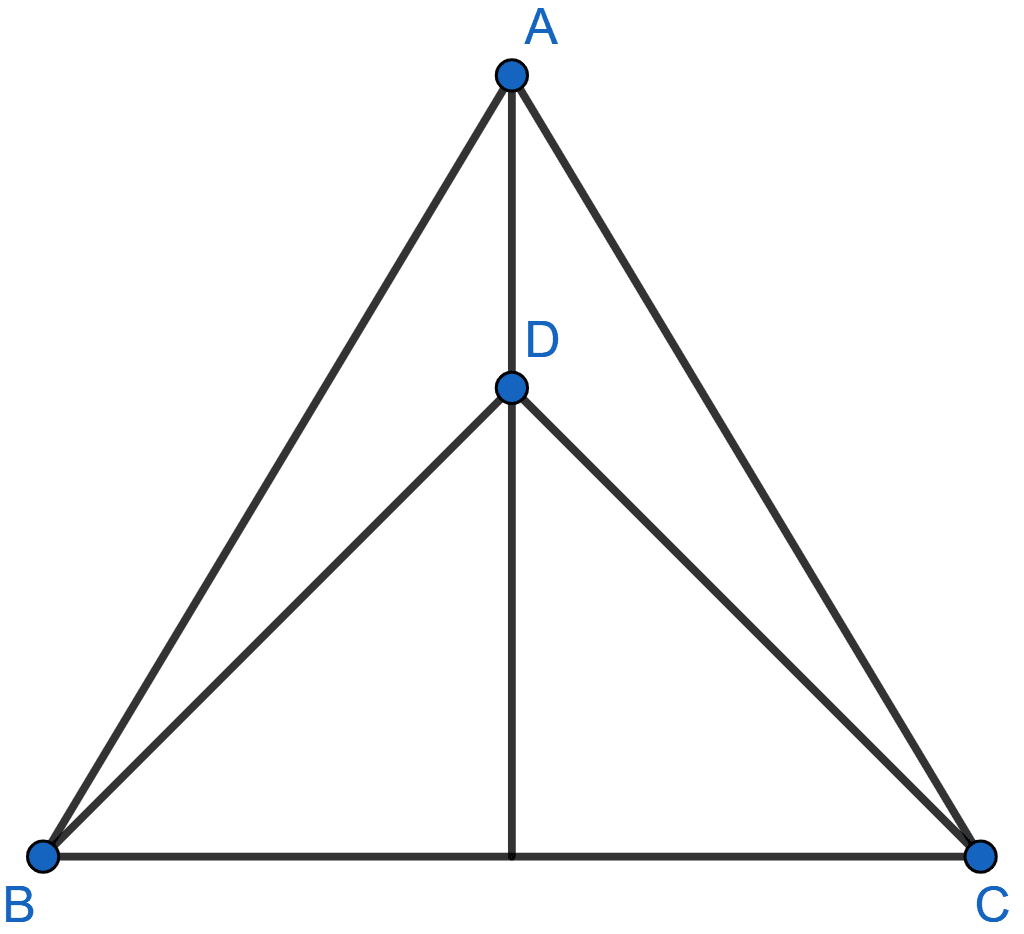
In the adjoining figure, AB = AC, D is a point in the interior of △ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of △ABC.
Answer
Given, AB = AC.
∴ ∠ABC = ∠ACB (As angles opposite to equal sides of isosceles triangle are equal.)
Given, ∠DBC = ∠DCB
∴ DB = DC. (Sides opposite to equal angles are equal.)
In △ABD and △ACD,
AB = AC (Given)
DB = DC (Proved)
AD = AD (Common)
Thus, △ABD ≅ △ACD by SSS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ ∠BAD = ∠CAD.
Hence, proved that AD bisects ∠BAC.
Related Questions
In the adjoining figure, OA ⊥ OD, OC ⊥ OB, OD = OA and OB = OC. Prove that AB = CD.

In the adjoining figure, PQ || BA and RS || CA. If BP = RC, prove that:
(i) △BSR ≅ △PQC
(ii) BS = PQ
(iii) RS = CQ.

In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
In △ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that △CAE is isosceles.