Mathematics
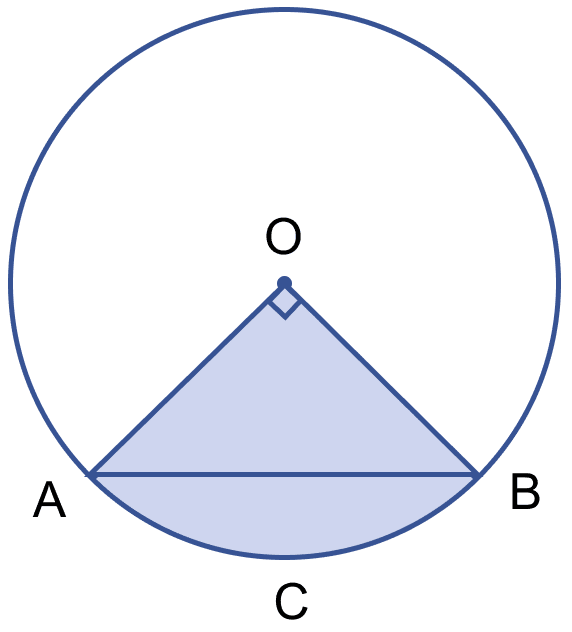
In the adjoining figure, a chord AB of a circle of radius 10 cm subtends a right angle at the centre O. Find the area of the sector OACB and of the major segment. Take π = 3.14.
Mensuration
Answer
Given,
Radius of the circle = 10 cm
Angle at the centre subtended by a chord AB = 90°.
We know that,
Area of sector OACB =
= 3.14 × 10 × 10 ×
=
= 78.5 cm2.
In right angle △OAB,
Area of △OAB = × OA × OB
= × 10 × 10
= 50 cm2.
Area of minor segment = Area of sector OACB – Area of △OAB
= 78.5 - 50
= 28.5 cm2.
Area of circle = πr2
= 3.14 × 10 × 10
= 314 cm2.
Area of major segment = Area of circle – Area of minor segment
= 314 - 28.5
= 285.5 cm2.
Hence, area of sector OACB = 78.5 cm2 and area of major segment = 285.5 cm2.
Answered By
Related Questions
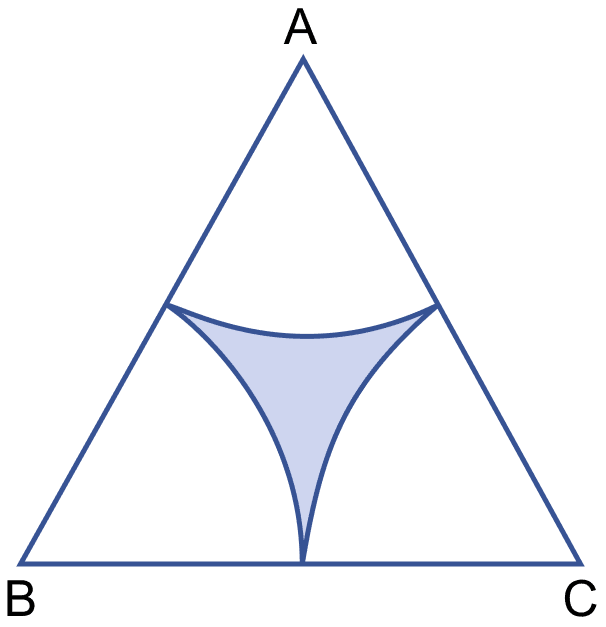
In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centers of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places.
A circle is inscribed in a regular hexagon of side cm. Find
(i) the circumference of the inscribed circle
(ii) the area of the inscribed circle
Find the surface area and volume of a cube whose one edge is 7 cm.
Find the surface area and the volume of a rectangular solid measuring 5 m by 4 m by 3 m. Also find the length of a diagonal.