Mathematics
In quadrilateral ABCD; angle D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm. Find the radius of the circle.
Circles
3 Likes
Answer
We know that,
Tangents from an exterior point are equal in length.
From figure,

BQ and BR are tangents from B to the circle.
∴ BR = BQ = 27 cm.
CR = BC - BR = 38 - 27 = 11 cm.
Since, CR and CS are the tangents from C to the circle.
∴ CS = CR = 11 cm.
DS = DC - SC = 25 - 11 = 14 cm.
Since, DS and DP are the tangents from D to the circle.
∴ DP = DS = 14 cm.
Since, ∠D = 90°.
Also,
∠OPD = ∠OSD = 90° [As, tangent to a point and radius from that point are perpendicular to each other.]
In quadrilateral OPDS,
By angle sum property of quadrilateral,
⇒ ∠OPD + ∠PDS + ∠OSD + ∠POS = 360°
⇒ 90° + 90° + 90° + ∠POS = 360°
⇒ ∠POS = 360° - 270° = 90°.
∴ OPDS is a square.
∴ OS = DP = 14 cm.
Hence, radius = 14 cm.
Answered By
1 Like
Related Questions
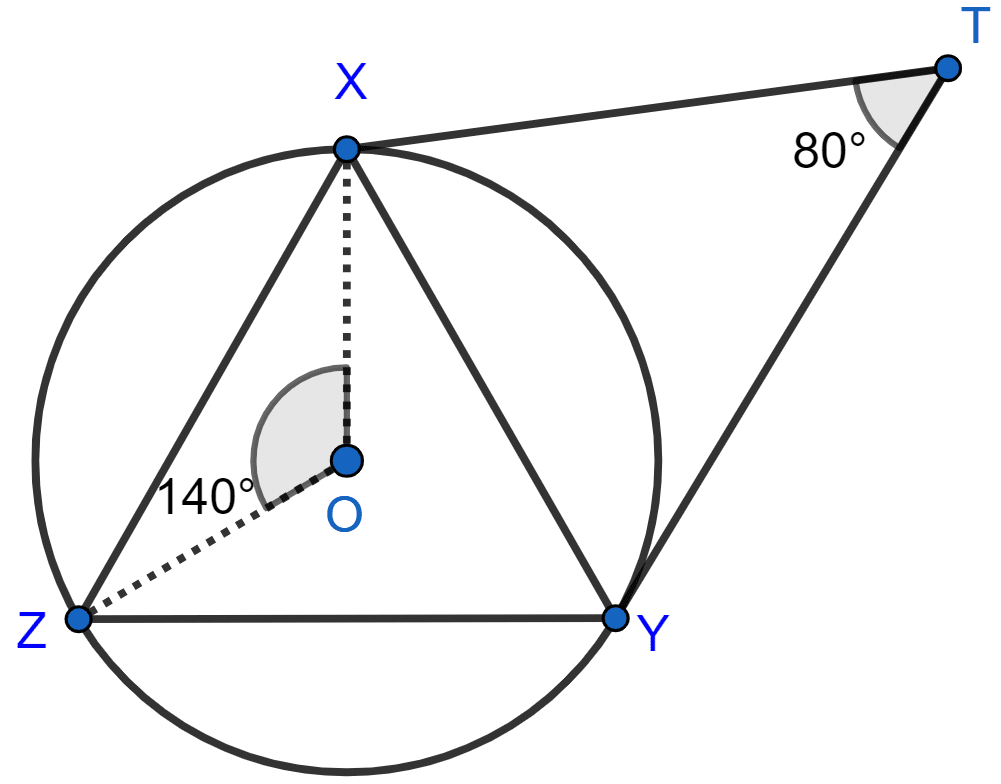
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

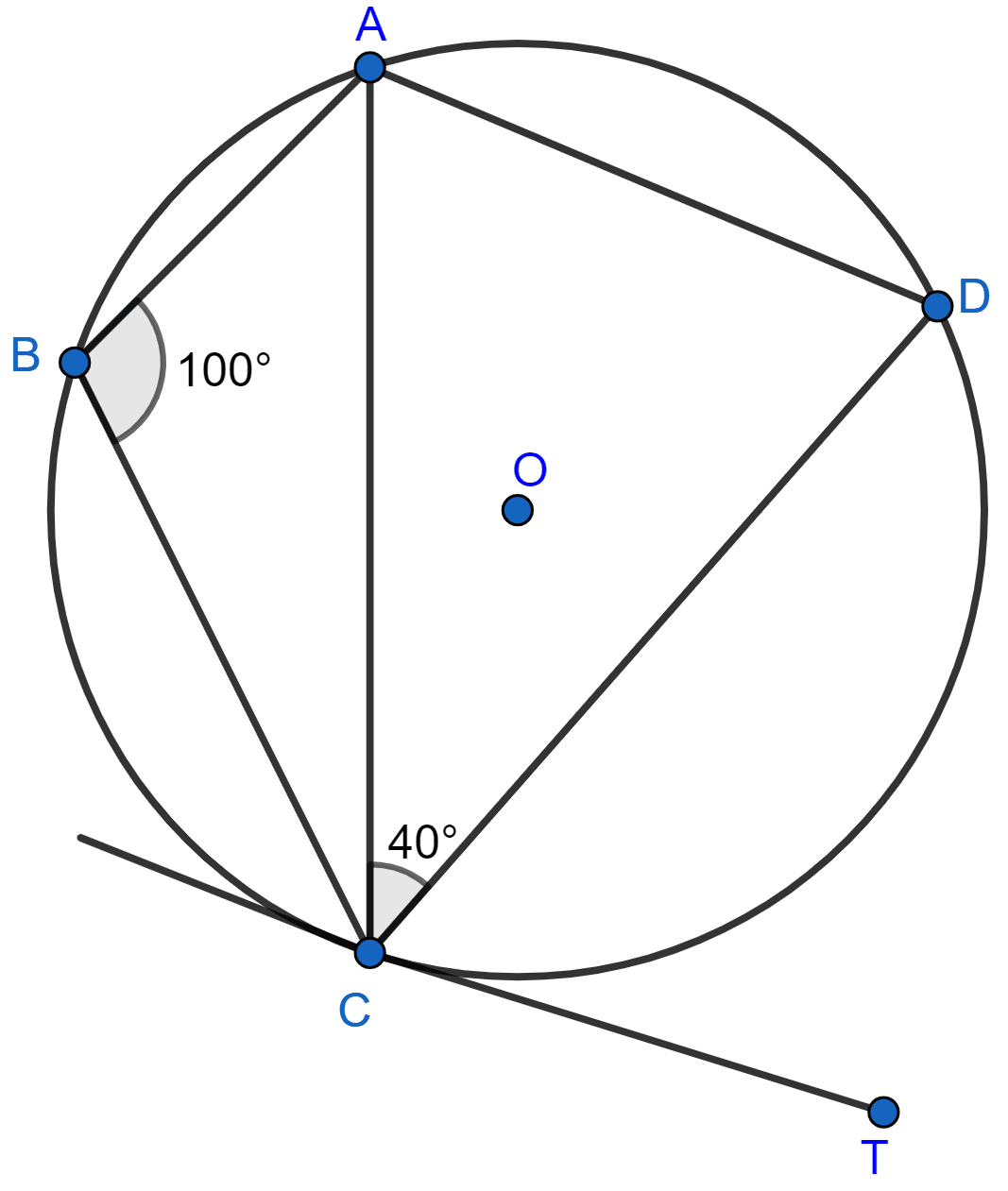
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
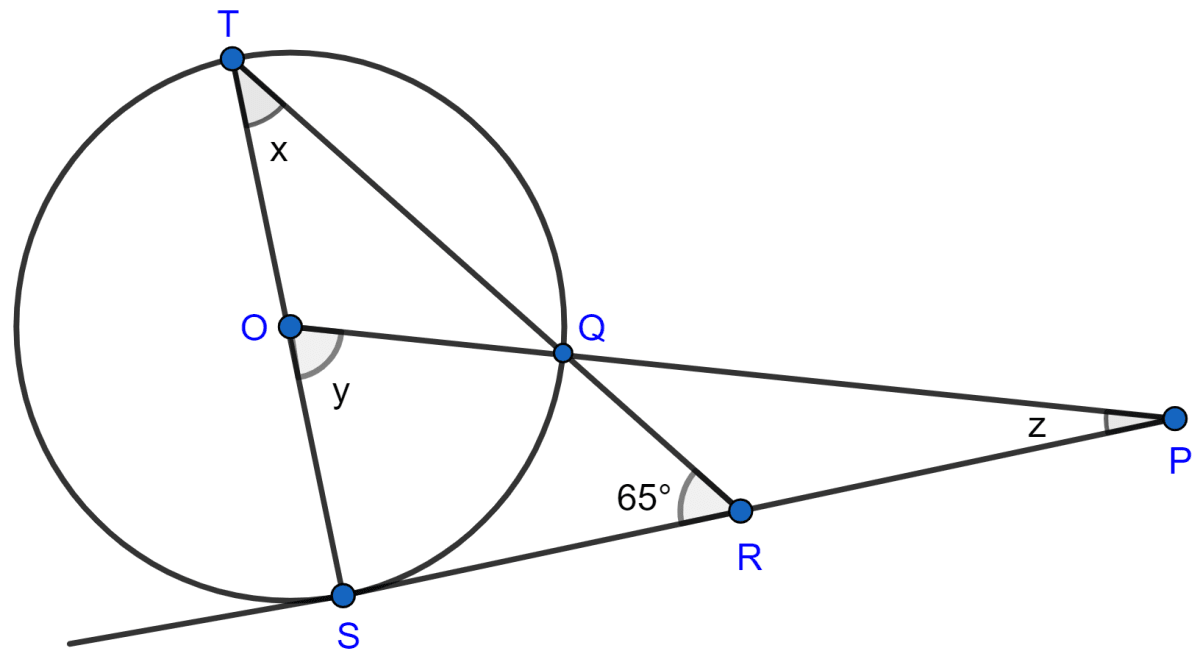
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.