Mathematics
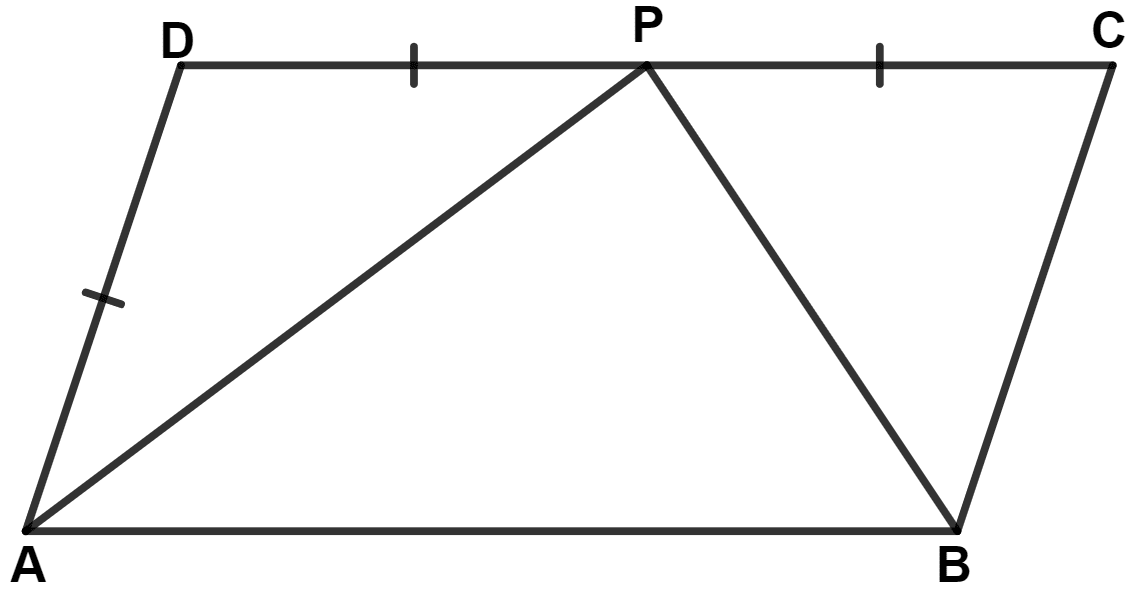
In parallelogram ABCD, the bisectors of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90°.
Related Questions
Prove that the bisectors of interior angles of a parallelogram form a rectangle.
Prove that the bisectors of the interior angles of a rectangle form a square.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
In the following figure, ABCD is a parallelogram. Prove that :
(i) AP bisects angle A
(ii) BP bisects angle B
(iii) ∠DAP + ∠CBP = ∠APB