Mathematics
In figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC; find x if radius of incircle is 10 cm.
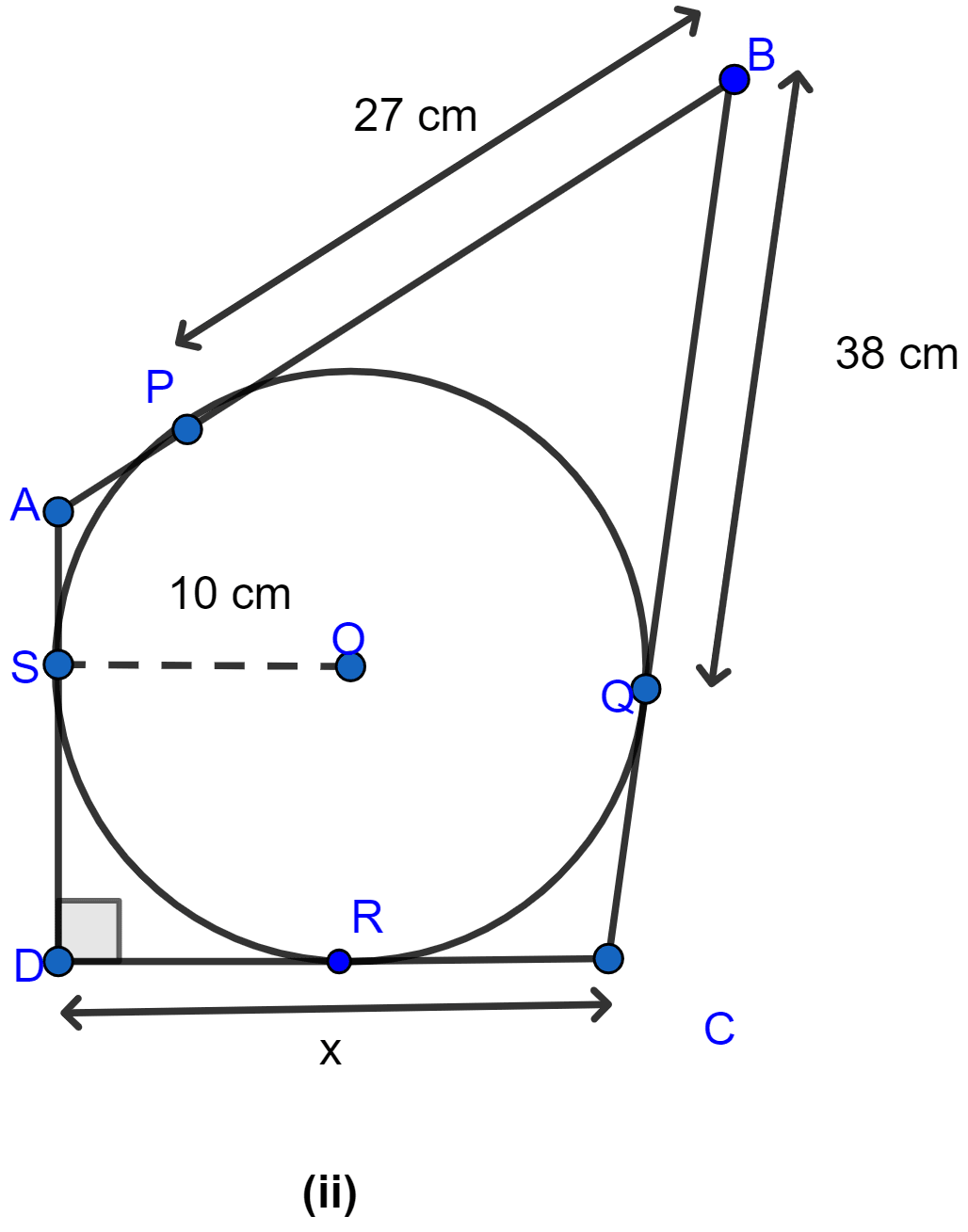
Answer
Join OR as shown in the figure below:
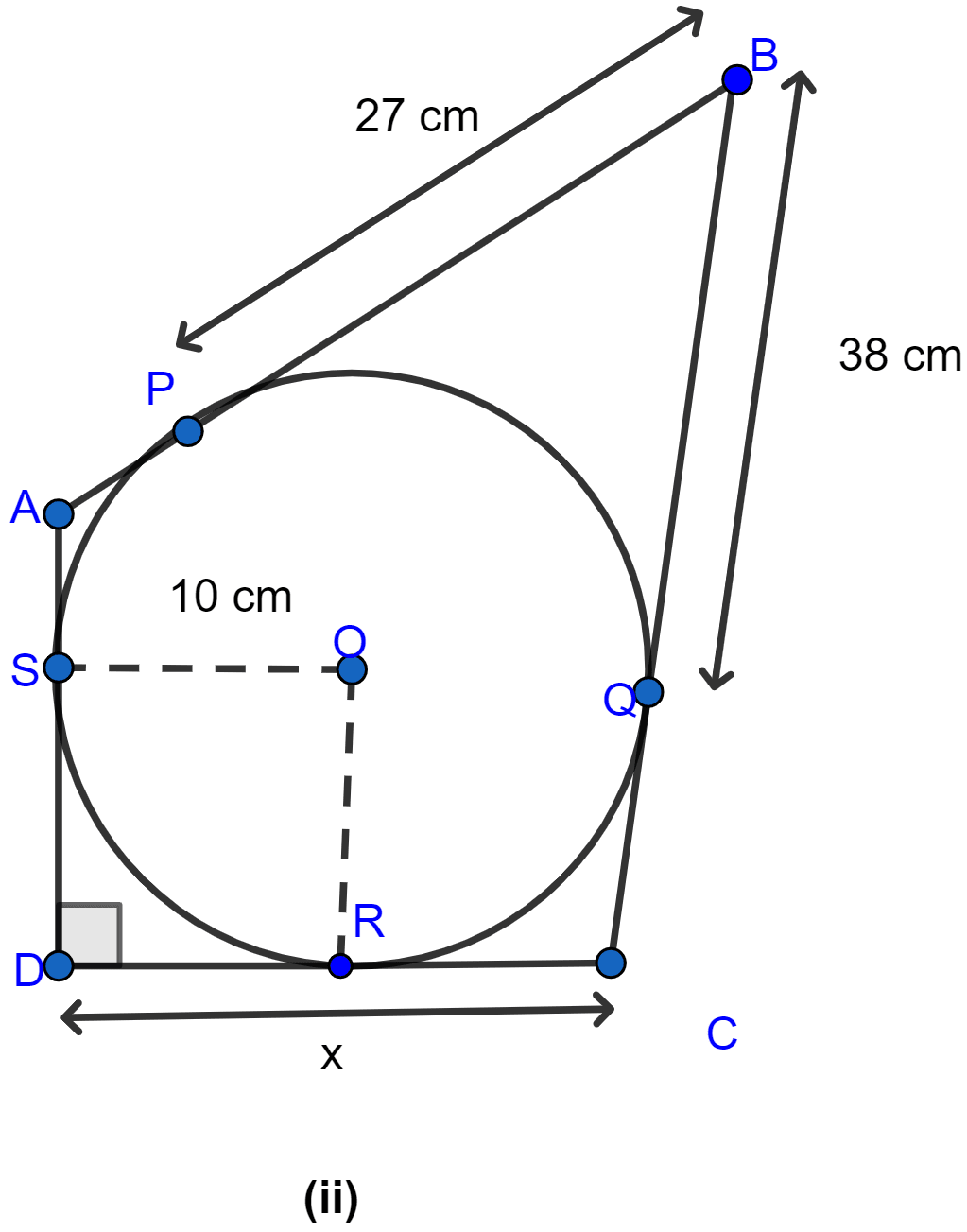
From figure,
OS = OR (As both are radius of circle.)
SD = OR (As OSDR form a square.)
∴ SD = OS.
From D, DS and DR are the tangents to the circle.
∴ DR = DS = 10 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From B, BP and BQ are the tangents to the circle.
∴ BQ = BP = 27 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
CQ = BC - BQ = 38 - 27 = 11 cm.
Now from C, CQ and CR are the tangents to the circle
CR = CQ = 11 cm.
⇒ DC = x = DR + CR = 10 + 11 = 21 cm.
Hence, the length of x = 21 cm.
Related Questions
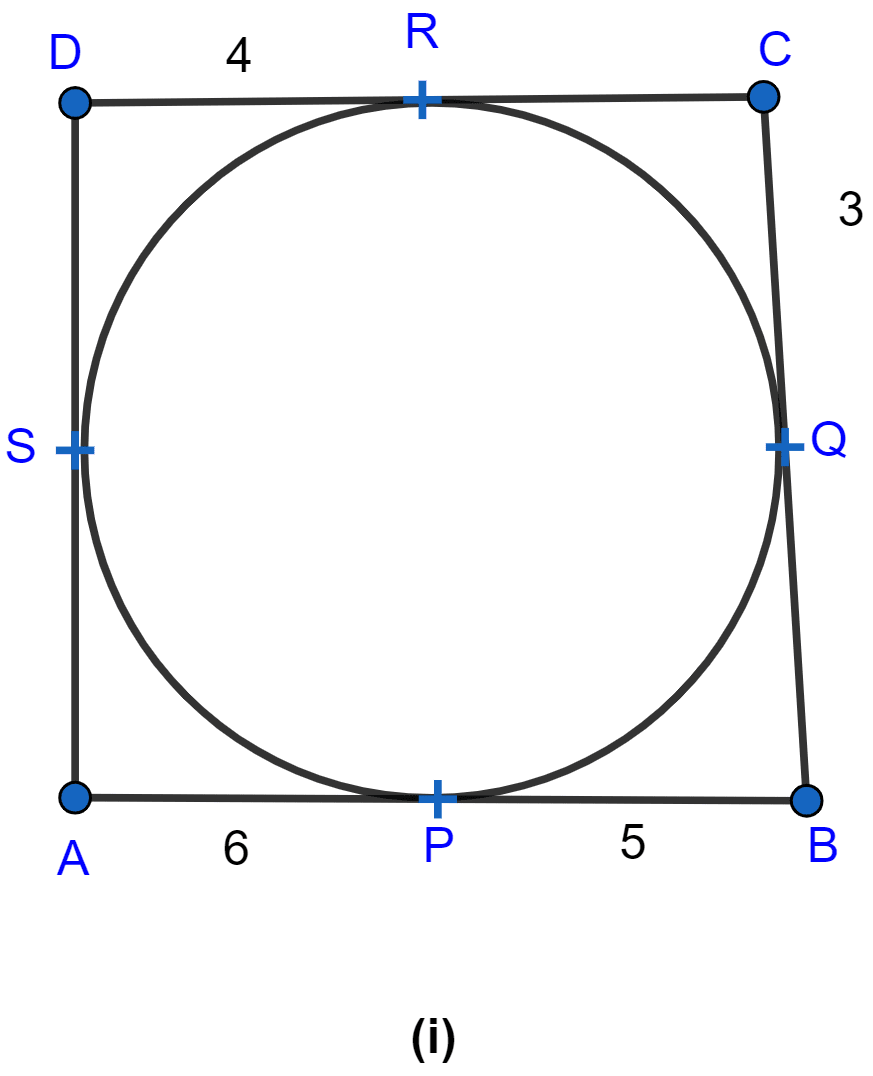
In figure (i) given below, quadrilateral ABCD is circumscribed ; find the perimeter of quadrilateral ABCD.
In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.
In figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.
In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.
