Mathematics

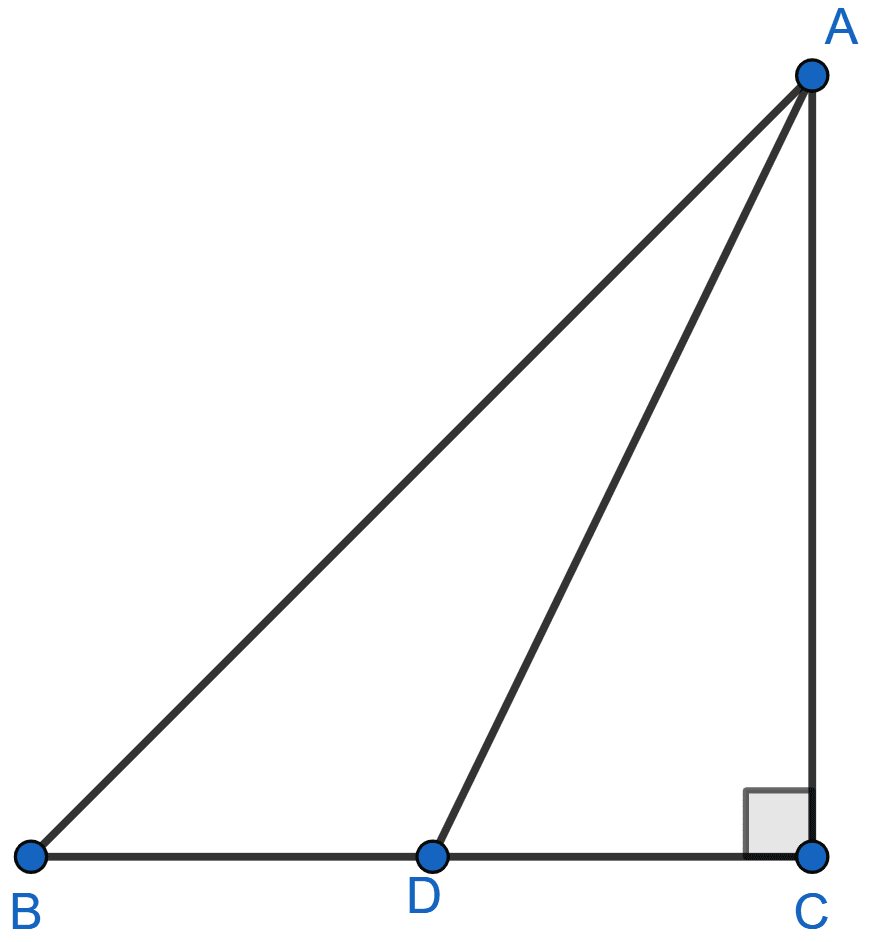
In figure given below, ∠D = 90°, AB = 16 cm, BC = 12 cm and CA = 6 cm. Find CD.

Pythagoras Theorem

91 Likes

Answer

Let CD be x cm.

In right angle △ACD,

By pythagoras theorem,

⇒ AC² = AD² + CD²

⇒ 6² = AD² + x²

⇒ AD² = 36 - x² …….(i)

In right angle △ABD,

By pythagoras theorem,

⇒ AB² = AD² + BD²

⇒ 16² = (36 - x²) + (12 + x)²

⇒ 256 = 36 - x² + 144 + x² + 24x

⇒ 256 = 180 + 24x

⇒ 24x = 76

⇒ x = $\dfrac{76}{24} = 3\dfrac{1}{6}$ cm.

Hence, CD = $3\dfrac{1}{6}$ cm.

Answered By

57 Likes

Related Questions

In figure given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB² = 4AD² - 3AC².
View Answer