Mathematics
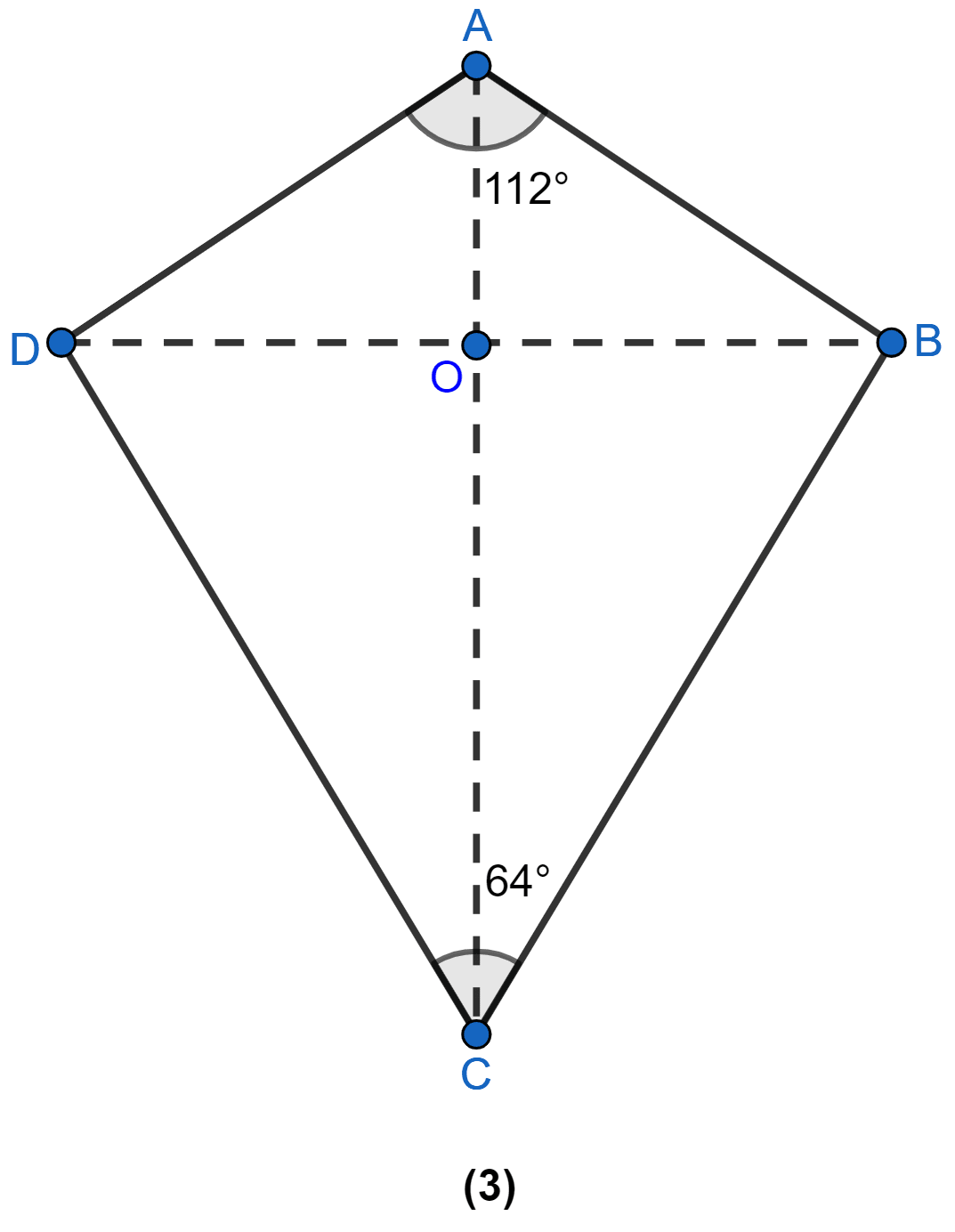
In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.
Rectilinear Figures
49 Likes
Answer
Diagonals of a kite bisect the vertex angles.
∴ ∠OCD = = 32° and ∠OAB = = 56°
Diagonals of a kite are perpendicular to each other.
∴ ∠DOC = 90°
⇒ ∠OCD + ∠DOC + ∠ODC = 180°
⇒ 32° + 90° + ∠ODC = 180°
⇒ ∠ODC = 58°.
Diagonals of a kite are perpendicular to each other.
∴ ∠AOB = 90°
⇒ ∠AOB + ∠OAB + ∠OBA = 180°
⇒ 90° + 56° + ∠OBA = 180°
⇒ ∠OBA = 180° - 146° = 34°.
Hence, ∠OBA = 34° and ∠ODC = 58°.
Answered By
27 Likes

