Mathematics
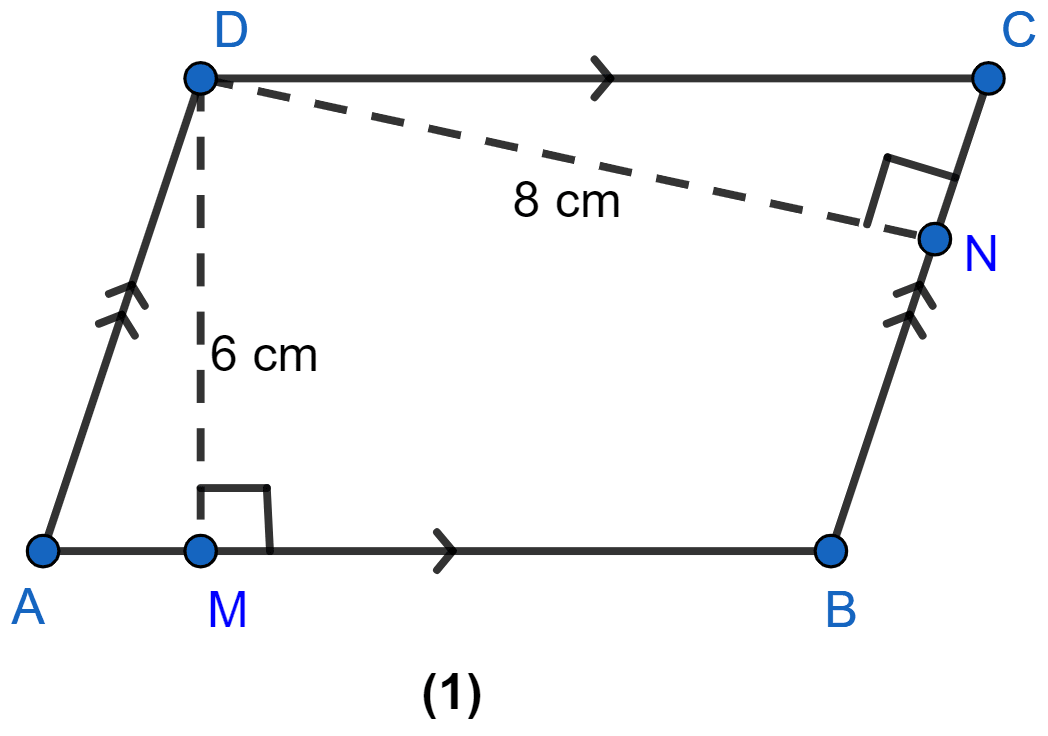
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.
Related Questions
ABCD is a rectangle and P is the mid-point of AB. DP is produced to meet CB at Q. Prove that the area of rectangle ABCD = area of ∆DQC.
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.
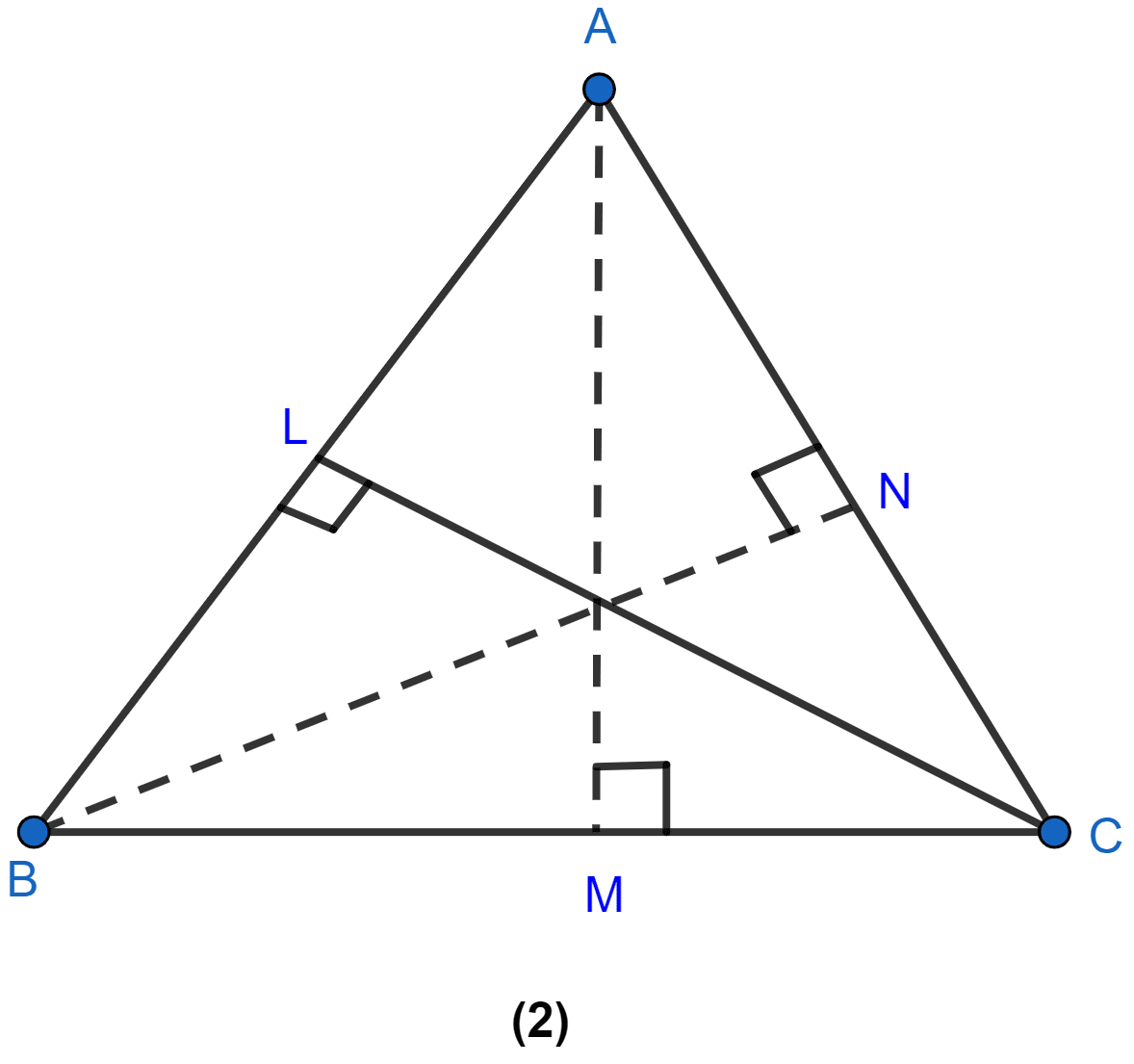
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
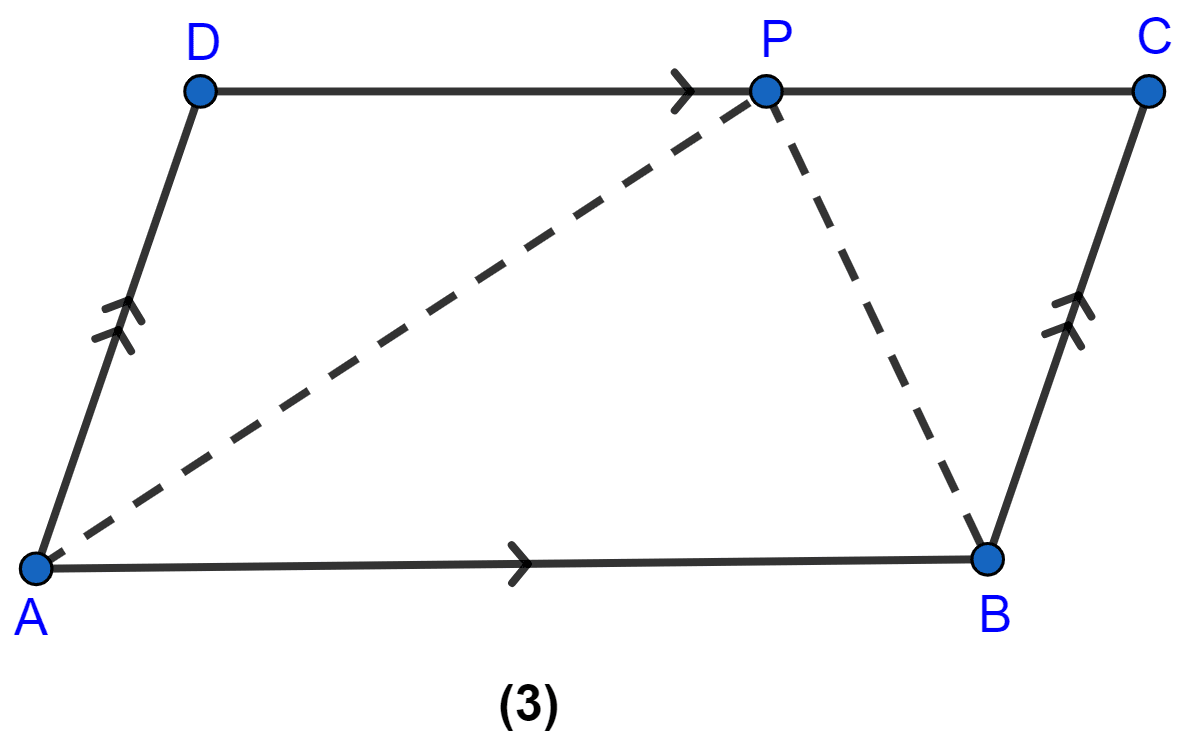
In the figure(3) given below, ABCD is a parallelogram. P is a point on DC such that area of ∆DAP = 25 cm2 and the area of ∆BCP = 15 cm2. Find
(i) area of || gm ABCD
(ii) DP : PC.
