Mathematics
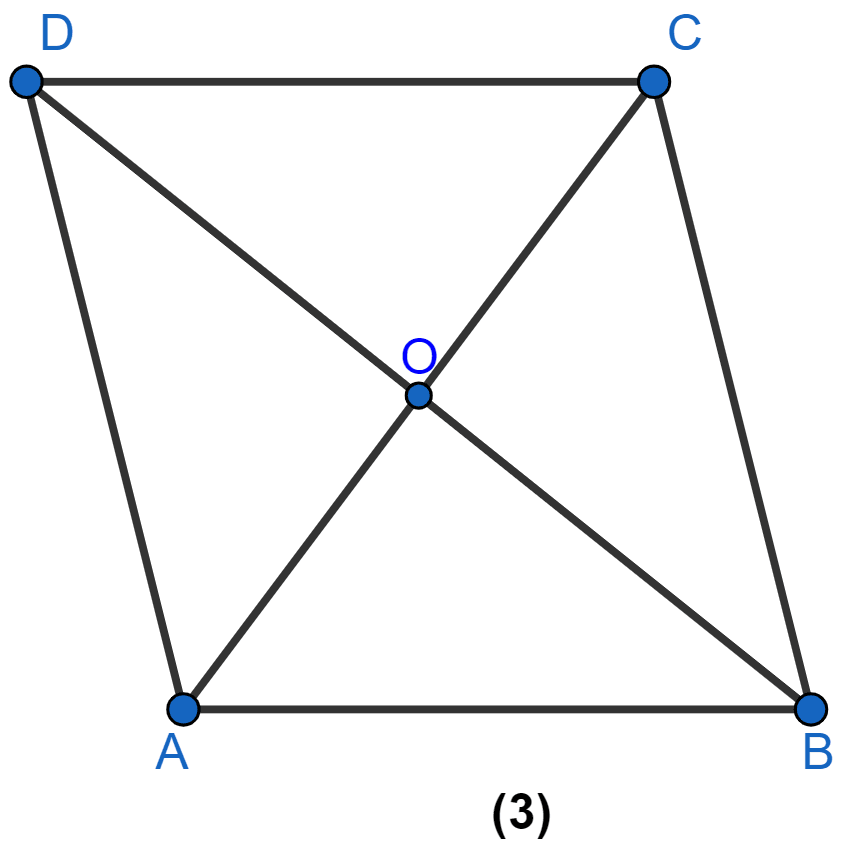
In figure (1) given below, equilateral triangle EBC surmounts square square ABCD. Find angle BED represented by x.
Answer
△EBC is an equilateral triangle, so all sides are equal.
EB = BC = EC ……..(i)
In square all sides are equal
AD = CD = BC = AB ……..(ii)
From (i) and (ii) we get,
BC = EC = CD
⇒ EC = CD.
In △ECD,
EC = CD
⇒ ∠DEC = ∠CDE = a (let) (Angles opposite to equal sides are equal in isosceles triangle)
⇒ ∠C = ∠ECB + ∠BCD
∠ECB = 60° (As each angle of a equilateral triangle = 60°)
∠BCD = 90° (As each angle of a square = 90°)
⇒ ∠C = 60° + 90° = 150°.
⇒ ∠DEC + ∠CDE + ∠C = 180
⇒ a + a + 150° = 180°
⇒ 2a = 180° - 150°
⇒ 2a = 30°
⇒ a = 15°.
From figure,
x° = ∠BEC - ∠DEC = 60° - 15° = 45°.
Hence, x = 45.
Related Questions
In figure (3) given below, ABCD is a rhombus. Find x and y.

The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, find ∠DPC.
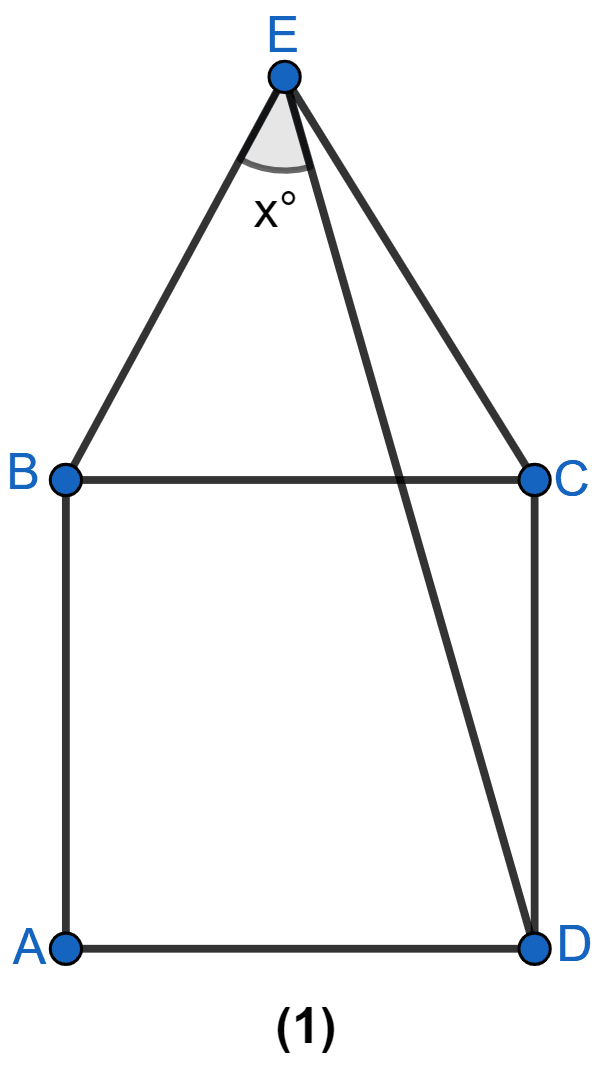
In Figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of △AOB.
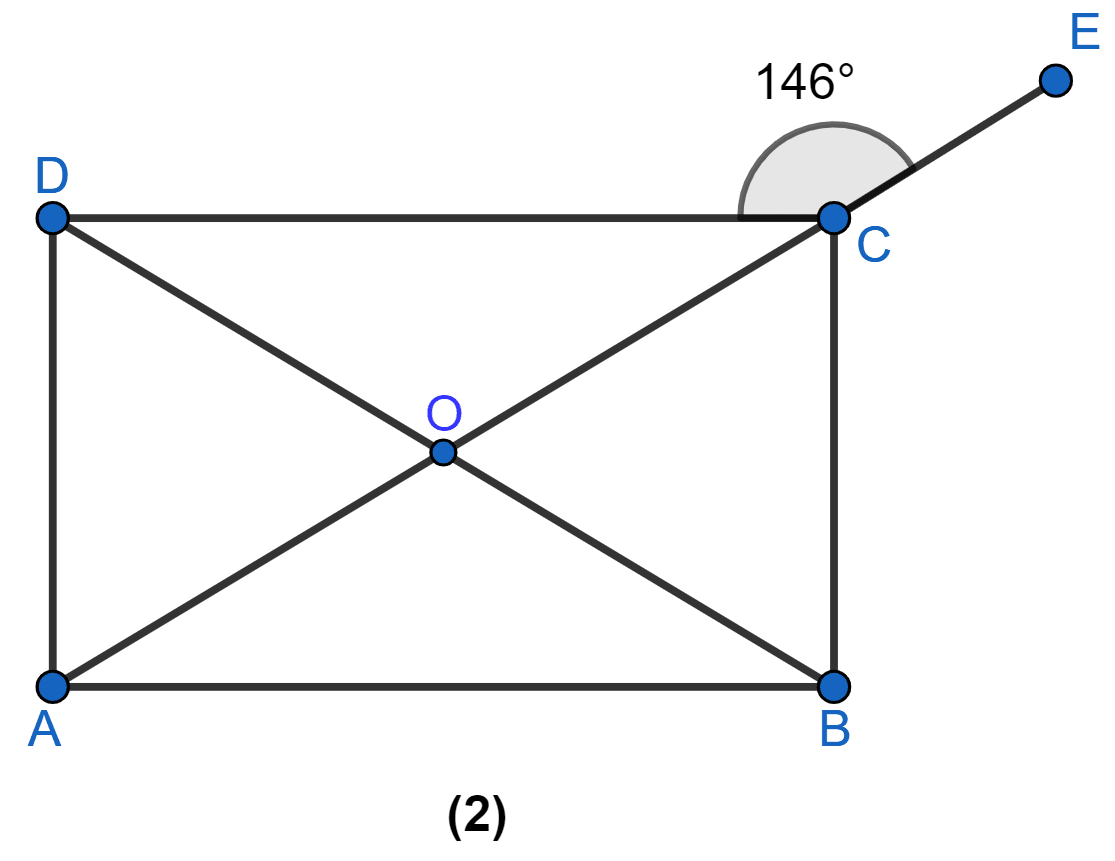
In figure (3) given below, ABCD is a rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3 : 2, find the angles of the △AOD.